题目内容
已知m2-m-1=0,求m5-5m-3的值.
考点:因式分解的应用
专题:
分析:先由已知条件得到m2=m+1,再利用因式分解,把m5-5m-3分解出m2出来,然后利用整体代入进行计算.
解答:解:∵m2-m-1=0,
∴m2=m+1,
∴m5-5m-3=m•m2•m2-5m+1
=m(m+1)•(m+1)-5m-3
=m(m2+2m+1)-5m-3
=m(m+1+2m+1)-5m-3
=3m2+2m-5m-3
=3(m+1)-3m-3
=3m+3-3m-3
=0.
∴m2=m+1,
∴m5-5m-3=m•m2•m2-5m+1
=m(m+1)•(m+1)-5m-3
=m(m2+2m+1)-5m-3
=m(m+1+2m+1)-5m-3
=3m2+2m-5m-3
=3(m+1)-3m-3
=3m+3-3m-3
=0.
点评:本题考查了因式分解的应用:利用因式分解解决求值问题;利用因式分解解决证明问题;利用因式分解简化计算问题.

练习册系列答案
相关题目
 在如图所示的直角坐标系中,解答下列问题:
在如图所示的直角坐标系中,解答下列问题: 如图,在Rt△ABC中,∠C=90°,AD是角平分线,且∠CED=∠CDE,求证:CF⊥AB.
如图,在Rt△ABC中,∠C=90°,AD是角平分线,且∠CED=∠CDE,求证:CF⊥AB.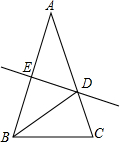 如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下述结论:①BD平分∠ABC;②AD=BD=BC;③△BDC的周长等于AB+BC;④D是AC中点.其中正确的命题序号是( )
如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下述结论:①BD平分∠ABC;②AD=BD=BC;③△BDC的周长等于AB+BC;④D是AC中点.其中正确的命题序号是( )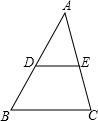 如图,在△ABC中,点D、E分别是AB、AC的中点,则下列结论:
如图,在△ABC中,点D、E分别是AB、AC的中点,则下列结论: