题目内容
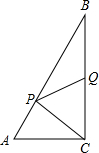 如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以5cm/s的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以4cm/s的速度向点B匀速运动,运动时间为ts(0<t<2),连接PQ.当△CPQ是以PC为腰的等腰三角形时,求t的值.
如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以5cm/s的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以4cm/s的速度向点B匀速运动,运动时间为ts(0<t<2),连接PQ.当△CPQ是以PC为腰的等腰三角形时,求t的值.考点:一元二次方程的应用
专题:几何动点问题
分析:过点P分别作PD⊥AC,垂足为D,PE⊥BC垂足为E,由题意得:BP=5t,CQ=4t,AP=10-5t,然后由PD∥BC,得到
=
=
,进而表示出PD=8-4t,AD=6-3t,然后分类:①当PQ为底时,求出t=
,②当QC为底时,求出t=
.
| AP |
| AB |
| PD |
| BC |
| AD |
| AC |
32-8
| ||
| 9 |
| 4 |
| 3 |
解答:解:过点P分别作PD⊥AC,垂足为D,PE⊥BC垂足为E,
由题意得:BP=5t,CQ=4t,
在Rt△ABC中,由勾股定理得:
AB2=BC2+AC2,
∴AB2=82+62,
∴AB=10,
∴AP=10-5t,
∵PD⊥AC,∠ACB=90°,
∴PD∥BC,
∴
=
=
,
即:
=
=
,
∴PD=8-4t,AD=6-3t,
∴DC=3t,
①当PQ为底时,PC=CQ,
即:PC2=CQ2,
∴PD2+CD2=CQ2,
即:(8-4t)2+(3t)2=(4t)2,
解得:t1=
>2(舍去),
t2=
,
②当QC为底时,PC=CQ,
∵PE⊥BC,
∴CE=
CQ=2t,
∵PD=CE,
∴8-4t=2t,
解得:t=
.
综上所述:当t=
或
时,△PCQ是以PC为腰的等腰三角形.

由题意得:BP=5t,CQ=4t,
在Rt△ABC中,由勾股定理得:
AB2=BC2+AC2,
∴AB2=82+62,
∴AB=10,
∴AP=10-5t,
∵PD⊥AC,∠ACB=90°,
∴PD∥BC,
∴
| AP |
| AB |
| PD |
| BC |
| AD |
| AC |
即:
| 10-5t |
| 10 |
| PD |
| 8 |
| AD |
| 6 |
∴PD=8-4t,AD=6-3t,
∴DC=3t,
①当PQ为底时,PC=CQ,
即:PC2=CQ2,
∴PD2+CD2=CQ2,
即:(8-4t)2+(3t)2=(4t)2,
解得:t1=
32+8
| ||
| 9 |
t2=
32-8
| ||
| 9 |
②当QC为底时,PC=CQ,
∵PE⊥BC,
∴CE=
| 1 |
| 2 |
∵PD=CE,
∴8-4t=2t,
解得:t=
| 4 |
| 3 |
综上所述:当t=
32-8
| ||
| 9 |
| 4 |
| 3 |

点评:此题考查一元二次方程的应用,涉及几何图形中的动点问题,此题注意分类讨论.

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
不用计算器,估算
的值应在( )
| 30 |
| A、5.0~5.5之间 |
| B、5.5~6.0之间 |
| C、6.0~6.5之间 |
| D、6.5~7.0之间 |
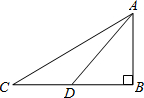 有一名码头工人站在码头上拉动一艘小船,此时绳子AC长20米,收取绳子5米时,小船向码头靠近了7米,此时船距码头几米?码头距水面有多高?
有一名码头工人站在码头上拉动一艘小船,此时绳子AC长20米,收取绳子5米时,小船向码头靠近了7米,此时船距码头几米?码头距水面有多高?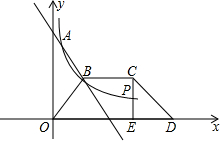 如图,直线y=ax+b与反比例函数y=
如图,直线y=ax+b与反比例函数y=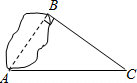 如图所示,为得到湖两岸A点和B点间的距离,一个观测者在C点设桩,使△ABC为直角三角形,并测得AC长20米,BC长16米,A、B两点间距离是多少?
如图所示,为得到湖两岸A点和B点间的距离,一个观测者在C点设桩,使△ABC为直角三角形,并测得AC长20米,BC长16米,A、B两点间距离是多少?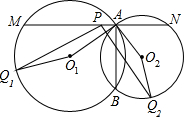 如图,已知⊙O1与⊙O2相交于A,B两点,直线MN⊥AB于A,且分别与⊙O1,⊙O2交于M、N,P为线段MN的中点,又∠AO1Q1=∠AO2Q2,求证:PQ1=PQ2.
如图,已知⊙O1与⊙O2相交于A,B两点,直线MN⊥AB于A,且分别与⊙O1,⊙O2交于M、N,P为线段MN的中点,又∠AO1Q1=∠AO2Q2,求证:PQ1=PQ2.