题目内容
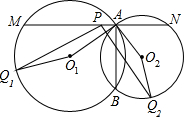 如图,已知⊙O1与⊙O2相交于A,B两点,直线MN⊥AB于A,且分别与⊙O1,⊙O2交于M、N,P为线段MN的中点,又∠AO1Q1=∠AO2Q2,求证:PQ1=PQ2.
如图,已知⊙O1与⊙O2相交于A,B两点,直线MN⊥AB于A,且分别与⊙O1,⊙O2交于M、N,P为线段MN的中点,又∠AO1Q1=∠AO2Q2,求证:PQ1=PQ2.考点:四点共圆,线段垂直平分线的性质,圆周角定理,圆内接四边形的性质,平行线分线段成比例
专题:证明题
分析:连接MQ1、BQ1、BQ2、NQ2,过点P作PH⊥Q1B于H,利用圆内接四边形的性质和圆周角定理可证到Q1、B、Q2三点共线,MQ1∥NQ2,进而可证到MQ1∥PH∥NQ2,然后根据平行线分线段成比例可得H为线段Q1Q2的中点,然后利用线段垂直平分线的性质就可证到结论.
解答:解:连接MQ1、BQ1、BQ2、NQ2,过点P作PH⊥Q1B于H,如图所示.
则由圆内接四边形的性质可得:
∠Q1MA+∠ABQ1=180°,∠ABQ2+∠ANQ2=180°,∠MAB=∠BQ2N.
由圆周角定理可得:
∠ABQ1=
∠AO1Q1,∠ANQ2=
∠AO2Q2.
∵∠AO1Q1=∠AO2Q2,
∴∠ABQ1=∠ANQ2,
∴∠ABQ2+∠ABQ1=∠ABQ2+∠ANQ2=180°,
∴Q1、B、Q2三点共线.
由圆内接四边形的性质可得:∠ABQ1=∠ANQ2,
∴∠Q1MA+∠ANQ2=∠Q1MA+∠ABQ1=180°,
∴MQ1∥NQ2.
∵AB⊥MN,
∴∠MAB=90°,
∴∠Q1Q2N=∠MAB=90°.
∵PH⊥Q1B,即∠Q1HP=90°,
∴∠Q1HP=∠Q1Q2N,
∴PH∥NQ2,
∴MQ1∥PH∥NQ2.
∵P为线段MN的中点,
∴H为线段Q1Q2的中点,
∴PH垂直平分Q1Q2,
∴PQ1=PQ2.
则由圆内接四边形的性质可得:
∠Q1MA+∠ABQ1=180°,∠ABQ2+∠ANQ2=180°,∠MAB=∠BQ2N.
由圆周角定理可得:
∠ABQ1=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠AO1Q1=∠AO2Q2,
∴∠ABQ1=∠ANQ2,
∴∠ABQ2+∠ABQ1=∠ABQ2+∠ANQ2=180°,
∴Q1、B、Q2三点共线.

由圆内接四边形的性质可得:∠ABQ1=∠ANQ2,
∴∠Q1MA+∠ANQ2=∠Q1MA+∠ABQ1=180°,
∴MQ1∥NQ2.
∵AB⊥MN,
∴∠MAB=90°,
∴∠Q1Q2N=∠MAB=90°.
∵PH⊥Q1B,即∠Q1HP=90°,
∴∠Q1HP=∠Q1Q2N,
∴PH∥NQ2,
∴MQ1∥PH∥NQ2.
∵P为线段MN的中点,
∴H为线段Q1Q2的中点,
∴PH垂直平分Q1Q2,
∴PQ1=PQ2.
点评:本题考查了圆内接四边形的性质、圆周角定理、平行线分线段成比例、线段垂直平分线的性质等知识,利用平行线分线段成比例是解决本题的关键,需要注意的是:只有证到Q1、B、Q2三点共线后,才能运用平行线分线段成比例.

练习册系列答案
相关题目
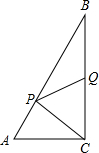 如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以5cm/s的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以4cm/s的速度向点B匀速运动,运动时间为ts(0<t<2),连接PQ.当△CPQ是以PC为腰的等腰三角形时,求t的值.
如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以5cm/s的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以4cm/s的速度向点B匀速运动,运动时间为ts(0<t<2),连接PQ.当△CPQ是以PC为腰的等腰三角形时,求t的值.