题目内容
11. 如图,在矩形ABCD中,已知AB=3,BC=4,将矩形ABCD绕着点D在桌面上顺针旋砖至A1B1C1D,使其停靠在矩形EFGH的点E处,若∠EDF=30°,则点B的运动路径长为( )
如图,在矩形ABCD中,已知AB=3,BC=4,将矩形ABCD绕着点D在桌面上顺针旋砖至A1B1C1D,使其停靠在矩形EFGH的点E处,若∠EDF=30°,则点B的运动路径长为( )| A. | $\frac{5}{6}$π | B. | $\frac{5}{3}$π | C. | $\frac{5}{2}$π | D. | $\frac{25}{3}$π |
分析 由在矩形ABCD中,已知AB=3,BC=4,可求得BD的长,由旋转的性质,易得∠BDC+∠B1DA1=90°,又由∠EDF=30°,即可求得∠BDB1的度数,继而求得答案.
解答 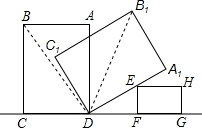 解:连接BD、B1D,
解:连接BD、B1D,
∵在矩形ABCD中,AB=3,BC=4,
∴CD=AB=3,
∴BD=$\sqrt{A{B}^{2}+C{D}^{2}}$=5,
根据旋转的性质可知:∠B1DA1=∠BDA,
根据矩形的性质可知:∠BDC+∠BDA=90°,
∴∠BDC+∠B1DA1=90°,
∵∠EDF=30°,
∴∠BDB1=180°-90°-30°=60°,
∴点B的运动路径长为:$\frac{60π×5}{180}$=$\frac{5π}{3}$.
故选B.
点评 此题考查了旋转的性质、矩形的性质以及勾股定理.注意求得∠BDB1的度数是解此题的关键.

练习册系列答案
相关题目
16.对于一次函数y=-3x+1,下列结论正确的是( )
| A. | y的值随x值的增大而增大 | B. | 图象与x轴的交点坐标是($\frac{1}{3}$,0) | ||
| C. | 它的图象经过第一、二、三象限 | D. | 图象与y轴的交点坐标是(0,-1) |
3. 如图,在同一平面内直线l∥m∥n,直线AB与直线l,m,n分别交于A,B,C三点,AB=BC,D为直线m上一点,∠ABD=40°,∠BAD=70°,若直线n上有一点E,BE=AD,则∠CEB的度数为( )
如图,在同一平面内直线l∥m∥n,直线AB与直线l,m,n分别交于A,B,C三点,AB=BC,D为直线m上一点,∠ABD=40°,∠BAD=70°,若直线n上有一点E,BE=AD,则∠CEB的度数为( )
 如图,在同一平面内直线l∥m∥n,直线AB与直线l,m,n分别交于A,B,C三点,AB=BC,D为直线m上一点,∠ABD=40°,∠BAD=70°,若直线n上有一点E,BE=AD,则∠CEB的度数为( )
如图,在同一平面内直线l∥m∥n,直线AB与直线l,m,n分别交于A,B,C三点,AB=BC,D为直线m上一点,∠ABD=40°,∠BAD=70°,若直线n上有一点E,BE=AD,则∠CEB的度数为( )| A. | 40°或70° | B. | 70° | C. | 110° | D. | 70°或110° |
 画出如图所示几何体的主视图、左视图、俯视图.
画出如图所示几何体的主视图、左视图、俯视图. 如图,∠A=∠OCD=90°,OA=2,OD=$\sqrt{7}$,AB=BC=CD=1,则△OBC形状直角三角形.
如图,∠A=∠OCD=90°,OA=2,OD=$\sqrt{7}$,AB=BC=CD=1,则△OBC形状直角三角形.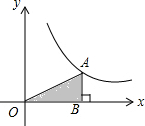 如图,已知双曲线y=$\frac{4}{x}$上有一点A,过A作AB垂直x轴于点B,连接OA,则△AOB的面积为( )
如图,已知双曲线y=$\frac{4}{x}$上有一点A,过A作AB垂直x轴于点B,连接OA,则△AOB的面积为( )