题目内容
17.已知关于x的方程x2+mx+m-2=0.(1)求证:无论m取何值时,方程总有两个不相等的实数根;
(2)设方程两实数根分别为x1,x2,且满足x12+x22=-3x1x2,求实数m的值.
分析 (1)先计算△=m2-4(m-2)=m2-4m+8,配方得到△=(m-2)2+4,由于(m-2)2≥0,则(m-2)2+4>0,即△>0,根据△的意义即可得到无论m取何值,该方程总有两个不相等的实数根;
(2)利用根与系数的关系,结合等式x12+x22=-3x1x2即可求解.
解答 (1)证明:∵△=m2-4×1×(m-2)=m2-4m+8=(m-2)2+4>0,
∴不论m取何实数,该方程都有两个不相等的实数根;
(2)解:x1+x2=-m,x1x2=m-2,
∵x12+x22=-3x1x2,
∴${{(x}_{1}{+x}_{2})}^{2}$-2x1 x2=-3x1 x2
∴${{(x}_{1}{+x}_{2})}^{2}$=-x1 x2
∴m2=2-m,
∴m2+m-2=0,
∴(m+2)(m-1)=0,
∴m=-2或1.
点评 本题主要考查一元二次方程根的判别式和根与系数的关系的应用,能够综合运用公式是解答此题的关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
5.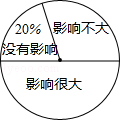 近年来,学校对“在初中数学教学时总使用计算器是否直接影响学生计算能力的发展”这一问题密切关注,为此,某校随机调查了n名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果绘制成如下不完整的统计表和扇形统计图,根据统计图表提供的信息,解答下列问题:
近年来,学校对“在初中数学教学时总使用计算器是否直接影响学生计算能力的发展”这一问题密切关注,为此,某校随机调查了n名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果绘制成如下不完整的统计表和扇形统计图,根据统计图表提供的信息,解答下列问题:
n名学生对这一问题的看法人数统计表
(1)求n的值;
(2)统计表中的m=100;
(3)估计该校1800名学生中认为“影响很大”的学生人数.
 近年来,学校对“在初中数学教学时总使用计算器是否直接影响学生计算能力的发展”这一问题密切关注,为此,某校随机调查了n名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果绘制成如下不完整的统计表和扇形统计图,根据统计图表提供的信息,解答下列问题:
近年来,学校对“在初中数学教学时总使用计算器是否直接影响学生计算能力的发展”这一问题密切关注,为此,某校随机调查了n名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果绘制成如下不完整的统计表和扇形统计图,根据统计图表提供的信息,解答下列问题:n名学生对这一问题的看法人数统计表
| 看法 | 没有影响 | 影响不大 | 影响很大 |
| 学生人数(人) | 40 | 60 | m |
(2)统计表中的m=100;
(3)估计该校1800名学生中认为“影响很大”的学生人数.
2.为了创建书香校园,切实引导学生多读书,读好书.某中学开展了“好书伴我成长”的读书节活动,为了了解本校学生每周课外阅读时间,随机抽取部分学生进行问卷调查,将课外阅读时间分为A、B、C、D四组,并利用臭氧所得的数据绘制了如下统计图.
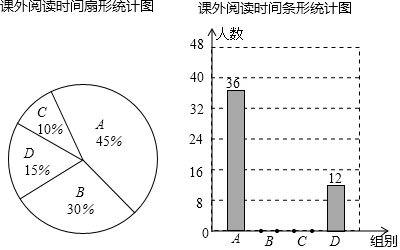
请根据图中提供的信息,解答下列问题:
(1)一共调查了80名学生;
(2)扇形统计图中A组的圆心角度数162°;
(3)直接补全条形统计图
(4)若该校有2400名学生,根据你所调查的结果,估计每周课外阅读时间不足3小时的学生有多少人?

| 组别 | 课外阅读t(单位:时) |
| A | X<2 |
| B | 2≤x<3 |
| C | 3≤x<4 |
| D | x≥4 |
(1)一共调查了80名学生;
(2)扇形统计图中A组的圆心角度数162°;
(3)直接补全条形统计图
(4)若该校有2400名学生,根据你所调查的结果,估计每周课外阅读时间不足3小时的学生有多少人?
7.在-3,2,-1,3这四个数中,比-2小的数是( )
| A. | -3 | B. | 2 | C. | -1 | D. | 3 |
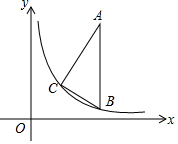 如图,在直角△ABC中,∠C=90°,∠A=30°,AB∥y轴,且AB=6,顶点B,C在反比例函数y=$\frac{k}{x}$(x>0)的图象上,且点B的横坐标为2$\sqrt{3}$,则k=$\sqrt{3}$.
如图,在直角△ABC中,∠C=90°,∠A=30°,AB∥y轴,且AB=6,顶点B,C在反比例函数y=$\frac{k}{x}$(x>0)的图象上,且点B的横坐标为2$\sqrt{3}$,则k=$\sqrt{3}$.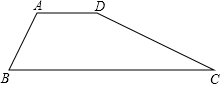 如图,已知四边形ABCD中,AD∥BC,AB=AD.
如图,已知四边形ABCD中,AD∥BC,AB=AD. 如图,AD是△ABC的角平分线,以AD为弦的⊙O交AB、AC于E、F,已知EF∥BC.
如图,AD是△ABC的角平分线,以AD为弦的⊙O交AB、AC于E、F,已知EF∥BC.