题目内容
19.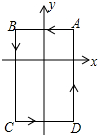 如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为2016个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A-…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是( )
如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为2016个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A-…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是( )| A. | (1,-1) | B. | (-1,1) | C. | (-1,-1) | D. | (0,-2) |
分析 根据点的坐标求出四边形ABCD的周长,然后求出另一端是绕第几圈后的第几个单位长度,从而确定答案.
解答 解:∵A(1,1),B(-1,1),C(-1,-2),D(1,-2),
∴AB=1-(-1)=2,BC=1-(-2)=3,CD=1-(-1)=2,DA=1-(-2)=3,
∴绕四边形ABCD一周的细线长度为2+3+2+3=10,
2016÷10=201余6,
∴细线另一端在绕四边形第202圈的第6个单位长度的位置,即CD中间的位置,
∴细线另一端所在位置的点的坐标为(0,-2),
故选:D.
点评 本题主要考查了点的坐标以及矩形的性质的运用,解决问题的关键是根据坐标求得四边形的周长并进行计算.解题时注意:矩形的对边相等.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
7.下列各数中,介于3和4之间的数是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{17}$ | C. | $\sqrt{12}$ | D. | $\root{3}{25}$ |
14.已知 A,B点的坐标分别是(-2,3)和(2,3),则下面四个结论:
①A、B关于x轴对称;②A、B关于y轴对称;③A点在第二象限,B点在第一象限;④A、B之间的距离为4.中正确的有( )
①A、B关于x轴对称;②A、B关于y轴对称;③A点在第二象限,B点在第一象限;④A、B之间的距离为4.中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.代数式a+$\frac{1}{2a}$,4xy,$\frac{a+b}{3}$,a,2016,$\frac{1}{2}$a2bc,-$\frac{3mn}{4}$中单项式的个数有( )
| A. | 6个 | B. | 5个 | C. | 4个 | D. | 3个 |
11.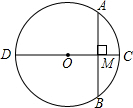 如图,⊙O的直径CD=10,弦AB=8,AB⊥CD,垂足为M,则DM的长为( )
如图,⊙O的直径CD=10,弦AB=8,AB⊥CD,垂足为M,则DM的长为( )
 如图,⊙O的直径CD=10,弦AB=8,AB⊥CD,垂足为M,则DM的长为( )
如图,⊙O的直径CD=10,弦AB=8,AB⊥CD,垂足为M,则DM的长为( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
8.四位同学画数轴如图所示,正确的是( )
| A. |  | B. |  | ||
| C. |  | D. |  |
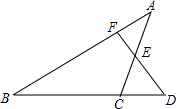 如图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E,∠A=35°,∠D=50°,求∠ACD的度数.
如图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E,∠A=35°,∠D=50°,求∠ACD的度数.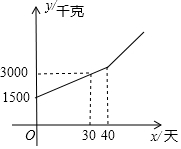 某块试验田里的农作物每天的需水量y(千克)与生长时间x(天)之间的关系如折线图所示.这些农作物在刚种植和第30天的需水量分别为1500千克和3000千克,在第40天后每天的需水量比前一天增加100千克.
某块试验田里的农作物每天的需水量y(千克)与生长时间x(天)之间的关系如折线图所示.这些农作物在刚种植和第30天的需水量分别为1500千克和3000千克,在第40天后每天的需水量比前一天增加100千克.