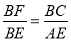题目内容
如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连接BG,DE.我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系.
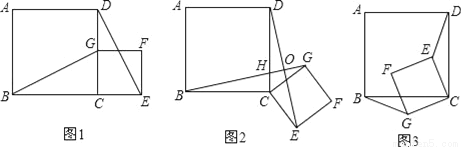
(1)猜想图1中线段BG、线段DE的长度关系及所在直线的位置关系;
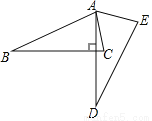
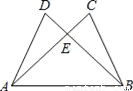
(2)将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度a,得到如图2、如图3情形.请你通过观察、测量等方法判断(1)中得到的结论是否仍然成立,并选取图2证明你的判断.
(1)BH⊥DE,即BG⊥DE,理由见解析. (2)BG=DE,BG⊥DE仍然成立,理由见解析. 【解析】试题分析:(1)根据正方形的性质,显然三角形BCG顺时针旋转90°即可得到三角形DCE,从而判断两条直线之间的关系; (2)结合正方形的性质,根据SAS仍然能够判定△BCG≌△DCE,从而证明结论. 【解析】 (1)BG=DE,BG⊥DE; ∵四边形ABCD和四...
练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
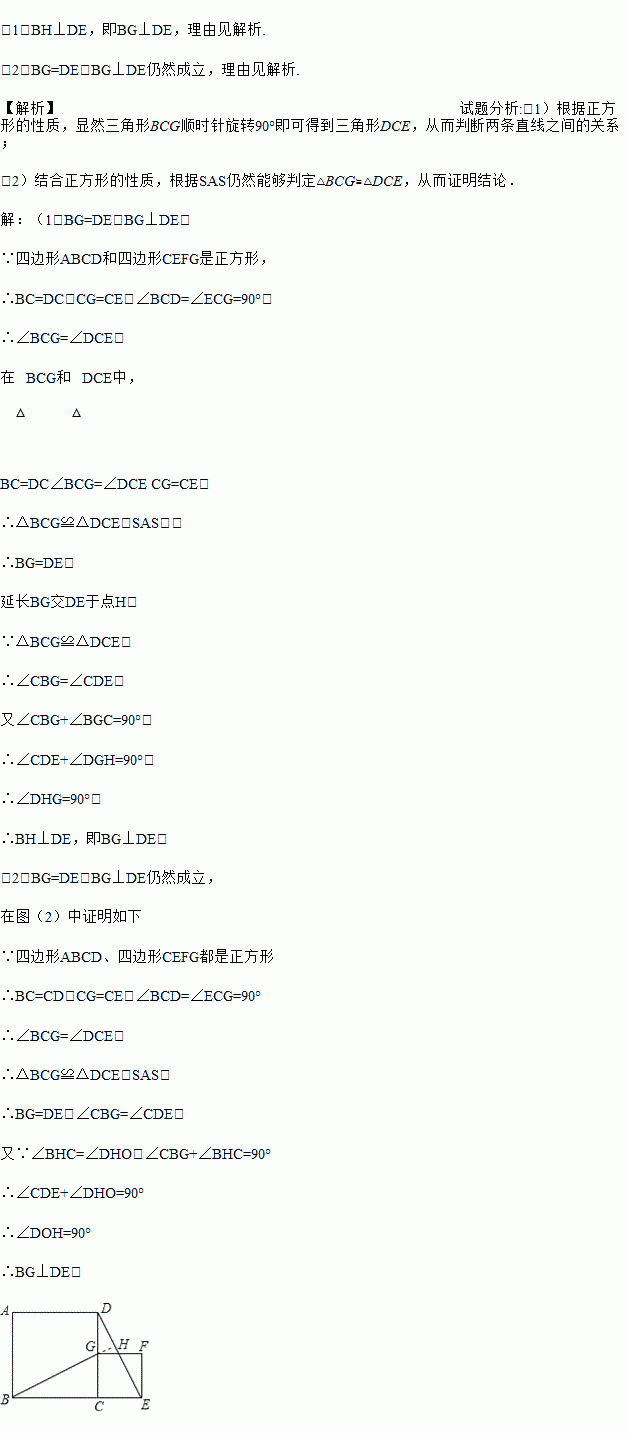

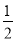 ∠BAC,AD平分∠BAC,若BC=6cm,则CD=_____cm。
∠BAC,AD平分∠BAC,若BC=6cm,则CD=_____cm。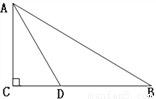
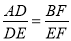 B.
B. 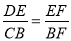 C.
C. 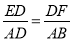 D.
D.