题目内容
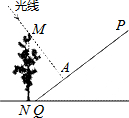
 已知:如图,斜坡MN坡度为i=1:2.4,在坡脚N处有一棵大树PN,太阳光线以30°的俯角将树顶P的影子落在斜坡MN上的点Q处.如果大树PN在斜坡MN上的影子NQ=13米,求大树PN的高度.
已知:如图,斜坡MN坡度为i=1:2.4,在坡脚N处有一棵大树PN,太阳光线以30°的俯角将树顶P的影子落在斜坡MN上的点Q处.如果大树PN在斜坡MN上的影子NQ=13米,求大树PN的高度.
分析:首先把实际问题转化为解直角三角形问题解决,作QA⊥PN于点A,QB⊥NB于点B(如图),根据坡度用QB表示出NB,再根据勾股定理求出QB、NB,则AQ=NB,在直角三角形PAQ中,由三角函数可求出PA,从而求出大树PN的高度.
解答: 解:作QA⊥PN于点A,QB⊥NB于点B,(如图)
解:作QA⊥PN于点A,QB⊥NB于点B,(如图)
∵斜坡MN坡度为i=1:2.4,
∴i=
=
,∴NB=2.4QB,
∵在Rt△QNB中,NQ=13米,
∴QB2+(2.4QB)2=132,
∴QB=5米,NB=12米.
在Rt△PAQ中,∵∠PQA=30°,AQ=NB=12米,
∴PA=AQ•tan30°=12×
=4
,
∴大树PN的高度PA+QB=(4
+5)米.
 解:作QA⊥PN于点A,QB⊥NB于点B,(如图)
解:作QA⊥PN于点A,QB⊥NB于点B,(如图)∵斜坡MN坡度为i=1:2.4,
∴i=
| QB |
| NB |
| 1 |
| 2.4 |
∵在Rt△QNB中,NQ=13米,
∴QB2+(2.4QB)2=132,
∴QB=5米,NB=12米.
在Rt△PAQ中,∵∠PQA=30°,AQ=NB=12米,
∴PA=AQ•tan30°=12×
| ||
| 3 |
| 3 |
∴大树PN的高度PA+QB=(4
| 3 |
点评:此题考查的知识点是解直角三角形的应用-坡度坡角问题,解题的关键是先转化为解直角三角形问题,主要是由勾股定理和三角函数求解.

练习册系列答案
相关题目
 已知,如图,斜坡PQ坡度为i=1:
已知,如图,斜坡PQ坡度为i=1: 已知:如图,斜坡MN坡度为i=1:2.4,在坡脚N处有一棵大树PN,太阳光线以30°的俯角将树顶P的影子落在斜坡MN上的点Q处.如果大树PN在斜坡MN上的影子NQ=13米,求大树PN的高度.
已知:如图,斜坡MN坡度为i=1:2.4,在坡脚N处有一棵大树PN,太阳光线以30°的俯角将树顶P的影子落在斜坡MN上的点Q处.如果大树PN在斜坡MN上的影子NQ=13米,求大树PN的高度.