题目内容
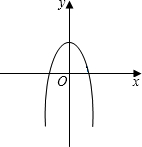
函数y=ax2+c（a≠0）的图象的对称轴是________；顶点坐标是________．
y轴 （0，c）
分析：由于抛物线顶点式y=a（x-h）2+k，顶点坐标是（h，k），对称轴是x=h，由此可以得到函数y=ax2+c（a≠0）的图象的对称轴，顶点坐标．
解答：根据抛物线顶点式y=a（x-h）2+k，
得函数y=ax2+c（a≠0）的图象的对称轴是y轴，顶点坐标是（0，c）．
故填空答案：y轴，（0，c）．
点评：求抛物线的顶点坐标、对称轴及最值通常有两种方法：
（1）公式法：y=ax2+bx+c的顶点坐标为（
，
），对称轴是x=；
（2）配方法：将解析式化为顶点式y=a（x-h）2+k，顶点坐标是（h，k），对称轴是x=h．
分析：由于抛物线顶点式y=a（x-h）2+k，顶点坐标是（h，k），对称轴是x=h，由此可以得到函数y=ax2+c（a≠0）的图象的对称轴，顶点坐标．
解答：根据抛物线顶点式y=a（x-h）2+k，
得函数y=ax2+c（a≠0）的图象的对称轴是y轴，顶点坐标是（0，c）．
故填空答案：y轴，（0，c）．
点评：求抛物线的顶点坐标、对称轴及最值通常有两种方法：
（1）公式法：y=ax2+bx+c的顶点坐标为（
，），对称轴是x=；（2）配方法：将解析式化为顶点式y=a（x-h）2+k，顶点坐标是（h，k），对称轴是x=h．
练习册系列答案
相关题目
15、函数y=ax2+bx+c的图象如图所示，且线段OM与ON相等，则a，b，c之间的关系为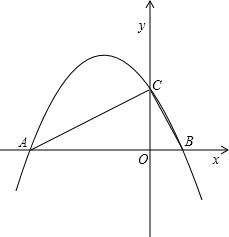
如图所示，二次函数y=ax2+bx+c（a≠0）的图象与x轴交于A、B两点，与y轴交于C（0，2），若∠ACB=90°，
如图，二次函数y=ax2+bx+c的图象与x轴交于B、C两点，与y轴交于点A（0，-3），∠ABC=45°，∠ACB=60°，求这个二次函数解析式．
已知正比例函数y=ax与反比例函数
