题目内容
7.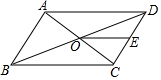 如图,?ABCD的对角线AC、BD相交于点O,点E是CD的中点,BC=10cm.求OE的长.
如图,?ABCD的对角线AC、BD相交于点O,点E是CD的中点,BC=10cm.求OE的长.
分析 先说明OE是△BCD的中位线,再根据三角形的中位线平行于第三边并且等于第三边的一半求解.
解答 解:∵?ABCD的对角线AC、BD相交于点O,
∴OB=OD,
∵点E是CD的中点,
∴CE=DE,
∴OE是△BCD的中位线,
∵BC=10cm,
∴OE=$\frac{1}{2}$BC=5cm.
点评 本题运用了平行四边形的对角线互相平分这一性质和三角形的中位线定理.

练习册系列答案
相关题目
17.下列运算中错误的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | $\sqrt{8}$÷$\sqrt{2}$=2 | C. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | D. | (-$\sqrt{3}$)2=3 |
2.计算2$\sqrt{12}$×$\frac{\sqrt{3}}{4}$÷$\sqrt{3}$的结果是( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{4}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
9.下列各题中,所求的最简公分母,错误的是( )
| A. | $\frac{1}{3x}$与$\frac{a}{6{x}^{2}}$最简公分母是6x2 | |
| B. | $\frac{1}{m+n}$与$\frac{1}{m-n}$的最简公分母是(m+n)(m-n) | |
| C. | $\frac{1}{3{a}^{2}{b}^{3}}$与$\frac{1}{3{a}^{2}{b}^{3}c}$最简公分母是3a2b3c | |
| D. | $\frac{1}{a(x-y)}$与$\frac{1}{b(y-x)}$的最简公分母是ab(x-y)(y-x) |
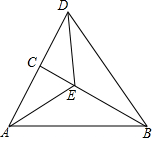 如图,已知在△ABC中,∠ACB=90°,∠BAC=60°,AE是∠BAC的平分线,延长AC至点D,使CD=AC.
如图,已知在△ABC中,∠ACB=90°,∠BAC=60°,AE是∠BAC的平分线,延长AC至点D,使CD=AC. 如图,∠DAC是△ABC的外角,且∠DAC=2∠B.
如图,∠DAC是△ABC的外角,且∠DAC=2∠B.