题目内容
4.若x2a+b-2xa-b+3=0是关于x的一元二次方程,求a,b的值.分析 本题根据一元二次方程的定义求解.分5种情况分别求解即可.
解答 解:∵x2a+b-2xa+b+3=0是关于x的一元二次方程,
∴①$\left\{\begin{array}{l}{2a+b=2}\\{a-b=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=1}\\{b=0}\end{array}\right.$;
②$\left\{\begin{array}{l}{2a+b=2}\\{a-b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=\frac{2}{3}}\\{b=\frac{2}{3}}\end{array}\right.$;
③$\left\{\begin{array}{l}{2a+b=1}\\{a-b=2}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=1}\\{b=-1}\end{array}\right.$;
④$\left\{\begin{array}{l}{2a+b=0}\\{a-b=2}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=\frac{2}{3}}\\{b=-\frac{4}{3}}\end{array}\right.$;
⑤$\left\{\begin{array}{l}{2a+b=2}\\{a-b=2}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=\frac{4}{3}}\\{b=-\frac{2}{3}}\end{array}\right.$;
综上所述$\left\{\begin{array}{l}{a=1}\\{b=0}\end{array}\right.$,$\left\{\begin{array}{l}{a=\frac{2}{3}}\\{b=\frac{2}{3}}\end{array}\right.$,$\left\{\begin{array}{l}{a=1}\\{b=-1}\end{array}\right.$,$\left\{\begin{array}{l}{a=\frac{2}{3}}\\{b=-\frac{4}{3}}\end{array}\right.$,$\left\{\begin{array}{l}{a=\frac{4}{3}}\\{b=-\frac{2}{3}}\end{array}\right.$.
点评 本题主要考查了一元二次方程的概念.解题的关键是分5种情况讨论x的指数.

 阅读快车系列答案
阅读快车系列答案| A. | 70×109 | B. | 0.7×109 | C. | 7×108 | D. | 7×109 |
| A. | x=0 | B. | x=2 | C. | x=4 | D. | x=8 |
| 选手 | 甲 | 乙 | 丙 | 丁 |
| 方差 | 0.035 | 0.016 | 0.022 | 0.025 |
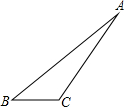 如图,AB=4,BC=1,∠B=45°,则△ABC的面积是$\sqrt{2}$.
如图,AB=4,BC=1,∠B=45°,则△ABC的面积是$\sqrt{2}$.