Question

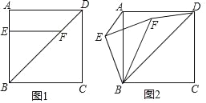
【题目】在四边形ABCD中，点E为AB边上的一点，点F为对角线BD上的一点，且EF⊥AB．若四边形ABCD为正方形．

①如图1，请直接写出AE与DF的数量关系　 　；

②将△EBF绕点B逆时针旋转到图2所示的位置，连接AE，DF，猜想AE与DF的数量关系并说明理由．

Answer 1

【答案】（1）FD＝AE；（2）DF＝AE

【解析】

（1）由正方形的性质可得AB=AD，∠ABD=45°，∠A=90°，可得BD=AB，由平行线分线段成比例可得，可得FD=AE；

（2）由旋转的性质可得∠ABE=∠DBF，，可证△ABE∽△DBF，可得FD=AE．

（1）∵四边形ABCD是正方形，

∴AB＝AD，∠ABD＝45°，∠A＝90°，

∴BD＝AB，

∵EF⊥AB，∠ABD＝45°

∴∠EFB＝45°＝∠ABD，

∴EF＝BE

∴BF＝BE，

∵∠A＝90°，EF⊥AB，

∴EF∥AD

∴

∴FD＝AE

（2）FD＝AE

理由如下：

∵旋转

∴∠ABE＝∠DBF，且

∴△ABE∽△DBF

∴

∴DF＝AE