题目内容
如图,AB是大半圆O的直径,AO是小半圆M的直径,点P是大半圆O上一点,PA与小半圆M交于点C,过点C作CD⊥OP于点D.
(1)求证:CD是小半圆M的切线;
(2)若AB=8,点P在大半圆O上运动(点P不与A,B两点重合),设PD=x,CD2=y.
①求y与x之间的函数关系式,并写出自变量x的取值范围;
②当y=3时,求P,M两点之间的距离.
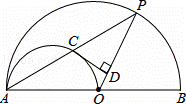
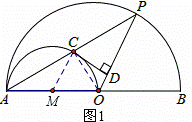
解:(1)连接CO、CM,如图1所示.
∵AO是小半圆M的直径,
∴∠ACO=90°即CO⊥AP.
∵OA=OP,
∴AC=PC.
∵AM=OM,
∴CM∥PO.
∴∠MCD=∠PDC.
∵CD⊥OP,
∴∠PDC=90°.
∴∠MCD=90°即CD⊥CM.
∵CD经过半径CM的外端C,且CD⊥CM,
∴直线CD是小半圆M的切线.
(2)①∵CO⊥AP,CD⊥OP,
∴∠OCP=∠ODC=∠CDP=90°.
∴∠OCD=90°﹣∠DCP=∠P.
∴△ODC∽△CDP.
∴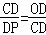 .
.
∴CD2=DP•OD.
∵PD=x,CD2=y,OP=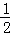 AB=4,
AB=4,
∴y=x(4﹣x)=﹣x2+4x.
当点P与点A重合时,x=0;当点P与点B重合时,x=4;
∵点P在大半圆O上运动(点P不与A,B两点重合),
∴0<x<4.
∴y与x之间的函数关系式为y=﹣x2+4x,
自变量x的取值范围是0<x<4.
②当y=3时,﹣x2+4x=3.
解得:x1=1,x2=3.
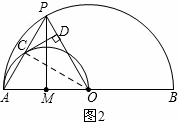
Ⅰ.当x=1时,如图2所示.
在Rt△CDP中,
∵PD=1,CD=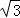 .
.
∴tan∠CPD=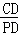 =
=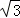 ,
,
∴∠CPD=60°.
∵OA=OP,
∴△OAP是等边三角形.
∵AM=OM,
∴PM⊥AO.
∴PM=
=
=2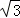 .
.
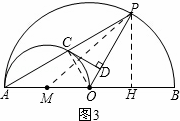
Ⅱ.当x=3时,如图3所示.
同理可得:∠CPD=30°.
∵OA=OP,
∴∠OAP=∠APO=30°.
∴∠POB=60°
过点P作PH⊥AB,垂足为H,连接PM,如图3所示.
∵sin∠POH=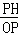 =
=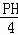 =
=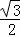 ,
,
∴PH=2 .
.
同理:OH=2.
在Rt△MHP中,
∵MH=4,PH=2 ,
,
∴PM=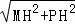
=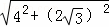
=2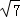 .
.
综上所述:当y=3时,P,M两点之间的距离为2 或2
或2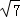 .
.

一次英语测试后,随机抽取九年级某班5名学生的成绩如下:91,78,98,85,98.关于这组数据说法正确的是( )
|
| A. | 中位数是91 | B. | 平均数是91 | C. | 众数是91 | D. | 极差是78 |
 、
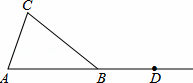
、 上,且
上,且 :
: =2:1,则△BDE与△ABC的面积比为何?
=2:1,则△BDE与△ABC的面积比为何?

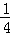 x2+
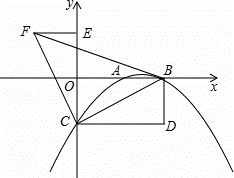
x2+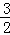 x﹣2交x轴于A,B两点(点A在点B的左侧),交y轴于点C,分别过点B,C作y轴,x轴的平行线,两平行线交于点D,将△BDC绕点C逆时针旋转,使点D旋转到y轴上得到△FEC,连接BF.
x﹣2交x轴于A,B两点(点A在点B的左侧),交y轴于点C,分别过点B,C作y轴,x轴的平行线,两平行线交于点D,将△BDC绕点C逆时针旋转,使点D旋转到y轴上得到△FEC,连接BF.