题目内容
【题目】如图，在四边形
中，
，连接
，
为上一点，连接
，过点
作
交于点
，则图中的全等三角形共有（ ）
A.4对B.3对C.2对D.1对
【答案】B
【解析】
先利用AAS证△ABF≌△CDE，利用全等性质得出AF=EC，推出AE=FC，再利用SAS证△ADE≌△CBF,利用SSS证△ABC≌△CDA,．
解：∵在四边形
中，
∴四边形是平行四边形
∴AB=CD
∠BAF=∠ECD
∵
∴∠DEF=∠BFE
∴在△ABF与△CDE
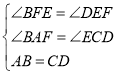
∴△ABF≌△CDE（AAS）
∴AF=EC,AB=CD
∴AF-EF=EC-EF即AE=FC
∵
∴∠DAE=∠FCB
∴在△ADE与△CBF
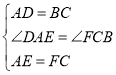
则△ADE≌△CBF（SAS）
在△ABC与△CDA
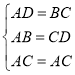
∴△ABC≌△CDA（SSS）
图中全等三角形有△ABF≌△CDE, △ADE≌△CBF, △ABC≌△CDA,共3对．
故选：B．
练习册系列答案
相关题目
