题目内容
4.(1)对于任意不相等的两个实数a、b,定义运算※如下:a※b=$\frac{\sqrt{a+b}}{a-b}$,例如3※2=$\frac{\sqrt{3+2}}{3-2}$=$\sqrt{5}$,求8※12的值.(2)先化简,再求值:$\frac{2}{a-1}$+$\frac{{a}^{2}-4a+4}{{a}^{2}-1}$÷$\frac{a-2}{a+1}$,其中a=1+$\sqrt{2}$.
分析 (1)根据运算的定义转化为根式的计算,然后对所求的式子进行化简;
(2)首先把所求的式子分子和分母分解因式,把除法转化为乘法,计算乘法,再进行分式的加法运算即可化简,最后代入数值计算即可.
解答 解:(1)原式=$\frac{\sqrt{8+12}}{8-12}$=$\frac{\sqrt{20}}{-4}$=-$\frac{\sqrt{5}}{2}$;
(2)原式=$\frac{2}{a-1}$+$\frac{(a-2)^{2}}{(a+1)(a-1)}$•$\frac{a+1}{a-2}$
=$\frac{2}{a-1}$+$\frac{a-2}{a-1}$
=$\frac{a}{a-1}$,
当a=1+$\sqrt{2}$时,原式=$\frac{1+\sqrt{2}}{\sqrt{2}}$=$\frac{2+\sqrt{2}}{2}$.
点评 本题考查了分式的化简求值,正确对分式的分子和分母分解因式是解题的关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
14.把二次函数y=2x2的图象向右平移3个单位,再向上平移2个单位后的函数关系式是( )
| A. | y=2(x-3)2+2 | B. | y=2(x+3)2+2 | C. | y=2(x-3)2-2 | D. | y=2(x+3)2-2 |
12.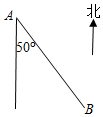 如图,货轮A与灯塔B相距20km,下列灯塔B相对于货轮A的位置的描述中,正确的是( )
如图,货轮A与灯塔B相距20km,下列灯塔B相对于货轮A的位置的描述中,正确的是( )
 如图,货轮A与灯塔B相距20km,下列灯塔B相对于货轮A的位置的描述中,正确的是( )
如图,货轮A与灯塔B相距20km,下列灯塔B相对于货轮A的位置的描述中,正确的是( )| A. | 南偏东50° | B. | 南偏东50°且距货轮20 km处 | ||
| C. | 距灯塔20 km处 | D. | 北偏西50°且距货轮20 km处 |
9.4的平方根是( )
| A. | 2 | B. | -2 | C. | ±2 | D. | ±$\frac{1}{2}$ |
16.一个三角形三个内角的度数比为1:2:1,这个三角形是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 等腰直角三角形 |
13.若关于x的方程2x+a-4=0的解是-2,则a的值等于( )
| A. | -8 | B. | 8 | C. | 0 | D. | 2 |
 分别从正面、左面和上面这三个方向看下面的四个几何体中的一个,得到如图所示的平面图形,那么这个几何体是( )
分别从正面、左面和上面这三个方向看下面的四个几何体中的一个,得到如图所示的平面图形,那么这个几何体是( )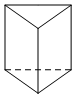
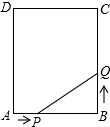 如图,矩形ABCD中,AB=6cm,BC=12cm,点P从A开始沿AB边向点B以1厘米/秒的速度移动,点Q从点B开始沿BC边向点C以2厘米/秒的速度移动.如果P、Q分别是从A、B同时出发,
如图,矩形ABCD中,AB=6cm,BC=12cm,点P从A开始沿AB边向点B以1厘米/秒的速度移动,点Q从点B开始沿BC边向点C以2厘米/秒的速度移动.如果P、Q分别是从A、B同时出发,