题目内容
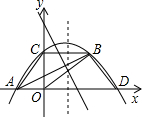
已知如图：（1）、（2）中各有两个三角形，其边长和角的度数已在图上标注，图（2）中AB、CD交于0点，对于各图中的两个三角形而言，下列说法正确的是
- A.都相似
- B.都不相似
- C.只有（1）相似
- D.只有（2）相似
A
分析：图（1）根据三角形的内角和定理，即可求得△ABC的第三角，由有两角对应相等的三角形相似，即可判定（1）中的两个三角形相似；
图（2）根据图形中的已知条件，即可证得
，又由对顶角相等，即可根据对应边成比例且夹角相等的三角形相似证得相似．
解答：如图（1）∵∠A=35°，∠B=75°，
∴∠C=180°-∠A-∠B=70°，
∵∠E=75°，∠F=70°，
∴∠B=∠E，∠C=∠F，
∴△ABC∽△DEF；
如图（2）∵OA=4，OD=3，OC=8，OB=6，
∴，
∵∠AOC=∠DOB，
∴△AOC∽△DOB．
故选A．
点评：此题考查了相似三角形的判定．注意有两角对应相等的三角形相似与对顶角相等，即可根据对应边成比例且夹角相等的三角形相似的定理的应用．
分析：图（1）根据三角形的内角和定理，即可求得△ABC的第三角，由有两角对应相等的三角形相似，即可判定（1）中的两个三角形相似；
图（2）根据图形中的已知条件，即可证得
，又由对顶角相等，即可根据对应边成比例且夹角相等的三角形相似证得相似．解答：如图（1）∵∠A=35°，∠B=75°，
∴∠C=180°-∠A-∠B=70°，
∵∠E=75°，∠F=70°，
∴∠B=∠E，∠C=∠F，
∴△ABC∽△DEF；
如图（2）∵OA=4，OD=3，OC=8，OB=6，
∴
，∵∠AOC=∠DOB，
∴△AOC∽△DOB．
故选A．
点评：此题考查了相似三角形的判定．注意有两角对应相等的三角形相似与对顶角相等，即可根据对应边成比例且夹角相等的三角形相似的定理的应用．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
过△ABC的三个顶点，已知如图，点C是线段AB的黄金分割点（AC＞BC），则下列结论中正确的是（ ）
| A、AB2=AC2+BC2 | ||||||
| B、BC2=AC•BA | ||||||
C、
| ||||||
D、
|
（2012•通州区一模）已知如图，在△ABC中，AB=AC，∠ABC=α，将△ABC以点B为中心，沿逆时针方向旋转α度（0°＜α＜90°），得到△BDE，点B、A、E恰好在同一条直线上，连接CE．
已知如图，菱形ABCD中，∠ADC=120°，BD=2