题目内容
被誉为东昌三宝之首的铁塔，始建于北宋时期，是我市现存的最古老的建筑。如图，已知测角仪AC高为1．6米，CD的长为6米，在C点测的塔顶E的仰角为45°，在D点测的塔顶E的仰角为60°,CD所在的水平线CG⊥EF于G,求铁塔EF的高。（结果精确到0．1米）
【答案】
15．8米
【解析】解：设EG=x米
在RT△CEG中，∵∠ECG=45°，∴∠CEG=45°，
∴∠ECG=∠CEG，∴CG=EG=x米。
在RT△DEG中, ∠EDG=60°，tan∠EDG=
,
∴DG=
∵CG-DG=CD=6, ∴x-
=6,
解得x=9+
∴EF=EG+GF=9++1．6≈15．8
所以铁塔的高约为15．8米
根据已知得出EG=CG，进而求出CD+DG=EG，再利用测角仪AC的高为1.6m，求出铁塔EF的高即可．
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
相关题目
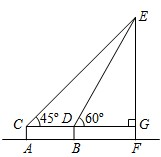（2011•聊城）被誉为东昌三宝之首的铁塔，始建于北宋时期，是我市现存的最古老的建筑．铁塔由塔身和塔座两部分组成．为了测得铁塔的高度，小莹利用自制的测角仪，在C点测得塔顶E的仰角为45°，在D点测得塔顶E的仰角为60°．已知测角仪AC的高为1.6m，CD的长为6m，CD所在的水平线CG⊥EF于点G．求铁塔EF的高（精确到0.1m）．
