题目内容
9. 完成求解过程,并写出括号里的理由:
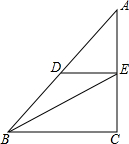
完成求解过程,并写出括号里的理由:如图,在直角△ABC中,∠C=90°,DE∥BC,BE平分∠ABC,∠ADE=40°,求∠BEC的度数.
解:∵DE∥BC(已知)
∴∠ABC=∠ADE=40°
∵BE平分∠ABC(已知)
∴∠CBE=$\frac{1}{2}$∠ABC=20度
∵在Rt△ABC中,∠C=90°(已知)
∴∠BEC=90°-∠CBE=70度.
分析 先根据平行线的性质求出∠ABC的度数,再由角平分线的性质求出∠CBE的度数,由直角三角形的性质即可得出∠BEC的度数.
解答 解:∵DE∥BC(已知)
∴∠ABC=∠ADE=40°
∵BE平分∠ABC(已知)
∴∠CBE=$\frac{1}{2}$∠ABC=20°.
∵在Rt△ABC中,∠C=90°(已知),
∴∠BEC=90°-∠CBE=70°.
故答案为:∠ABC,ABC,20,70.
点评 本题考查的是平行线的性质和三角形内角和定理,熟练掌握性质定理是解题的关键.

练习册系列答案
相关题目
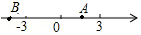 点A,B在数轴上的位置如图所示,其对应的数分别是a和b.对于以下结论:
点A,B在数轴上的位置如图所示,其对应的数分别是a和b.对于以下结论: