题目内容
已知抛物线y=x2+kx+1与x轴两个交点A、B都在原点左侧,顶点为C,△ABC是等腰直角三角形,求k的值.
考点:抛物线与x轴的交点
专题:
分析:设A(a,b),B(c,d)是抛物线y=x2+kx+1与x轴的两个交点,利用根与系数的关系以及完全平方公式的变形公式求得AB的长度;然后利用顶点坐标公式求得CD的长度;最后由“直角三角形斜边上的中线等于斜边的一半”列出关于k的方程,通过解方程来求k的值.
解答: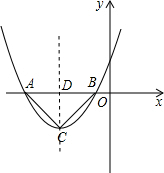 解:设A(a,b),B(c,d)是抛物线y=x2+kx+1与x轴的两个交点,
解:设A(a,b),B(c,d)是抛物线y=x2+kx+1与x轴的两个交点,
∴a+c=-k,ac=1,
∴AB=
=
∵抛物线的解析式为:y=x2+kx+1,
∴C(-
,
).
∵△ABC是等腰直角三角形,抛物线的顶点为C,
∴CD=
AB,即|
|=
解得 k1=2,k2=-2(舍去),
即k的值是2.
 解:设A(a,b),B(c,d)是抛物线y=x2+kx+1与x轴的两个交点,
解:设A(a,b),B(c,d)是抛物线y=x2+kx+1与x轴的两个交点,∴a+c=-k,ac=1,
∴AB=
| (a+c)2-4ac |
| k2-4 |
∵抛物线的解析式为:y=x2+kx+1,
∴C(-
| k |
| 2 |
| 4-k2 |
| 4 |
∵△ABC是等腰直角三角形,抛物线的顶点为C,
∴CD=
| 1 |
| 2 |
| 4-k2 |
| 4 |
| 1 |
| 2 |
| k2-4 |
解得 k1=2,k2=-2(舍去),
即k的值是2.
点评:本题考查了抛物线与x轴的交点,等腰直角三角形.求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.

练习册系列答案
相关题目
下列各数有两个有效数字的是( )
| A、31000 |
| B、0.450 |
| C、1.70×104 |
| D、0.0016 |
 如图,把长方形纸片ABCD纸沿对角线折叠,设重叠部分为△EBD,那么下列说法不正确的是( )
如图,把长方形纸片ABCD纸沿对角线折叠,设重叠部分为△EBD,那么下列说法不正确的是( )| A、△EBD是等腰三角形,EB=ED |
| B、折叠后∠ABE和∠CBD一定相等 |
| C、折叠后得到的图形是轴对称图形 |
| D、△EBA和△EDC一定是全等 |
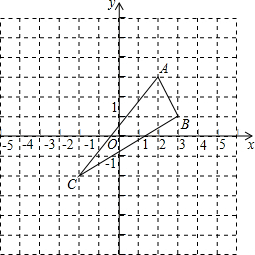 如图,已知△ABC的三个顶点分别为A(2,3)、B(3,1)、C(-2,-2).
如图,已知△ABC的三个顶点分别为A(2,3)、B(3,1)、C(-2,-2). 为了测量一棵树CD的高度,测量者在B点立一高位2m的标杆,测量者从E出可以看到A与C在同一直线上,若测得BD=23.6m,FB=3.2m,EF=1.6m,求树高.
为了测量一棵树CD的高度,测量者在B点立一高位2m的标杆,测量者从E出可以看到A与C在同一直线上,若测得BD=23.6m,FB=3.2m,EF=1.6m,求树高. 已知,如图,点E在AB上,点F是CD中点,EC∥BF,AD交EC、BF于点G、H,DC=8,
已知,如图,点E在AB上,点F是CD中点,EC∥BF,AD交EC、BF于点G、H,DC=8,