题目内容
已知：如图，在平行四边形ABCD中，AE⊥AC交AC于E，DF⊥AC交AC于F．
求证：BE=DF．
证明：∵AE⊥AC交AC于E，DF⊥AC交AC于F，
∴∠BEA=∠DFC=90°．
∵平行四边形ABCD，
∴AB∥CD，AB=CD．
∴∠BAE=∠DCF．
∴△ABE≌△CDF．
∴BE=DF．
分析：欲证BE=DF，先证明△ABE≌△CDF，可根据平行四边形的定义和性质结合三角形全等得出．
点评：本题可根据平行四边形的定义和性质结合三角形全等来解决有关的计算和证明．
∴∠BEA=∠DFC=90°．
∵平行四边形ABCD，
∴AB∥CD，AB=CD．
∴∠BAE=∠DCF．
∴△ABE≌△CDF．
∴BE=DF．
分析：欲证BE=DF，先证明△ABE≌△CDF，可根据平行四边形的定义和性质结合三角形全等得出．
点评：本题可根据平行四边形的定义和性质结合三角形全等来解决有关的计算和证明．
练习册系列答案
名校课堂系列答案
相关题目
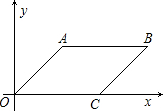如图，在平行四边形ABC0中，已知点A、C两点的坐标为A（
（2013•南平模拟）如图，已知四边形ABCD．请在下列四个关系中，选出两个恰当的关系作为条件，推出四边形ABCD是平行四边形，并予证明．
如图，在平行四边形OABC中，已知点A、C两点的坐标为A （
3，
，将∠OBA对折，使点O的对应点H恰好落在直线AB上，折痕交x轴于点C，