Question

【题目】如图，在矩形中，点为对角线的中点，过点作交于点，交于点，连接，．

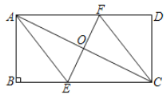
(1)求证：四边形是菱形；

(2)连接，若，，求的长．

Answer 1

【答案】（1）见解析 （2）

【解析】

（1）由矩形的性质可得∠ACB=∠DAC，然后利用“ASA”证明△AOF和△COE全等，根据全等三角形对应边相等可得OE=OF，即可证四边形AECF是菱形；

（2）连接BD，，根据平行四边形的性质可得AF=CF=10，用勾股定理求得FD=6，在△BDC中，∠DCB=90°，用勾股定理求出BD的值，即可解答.

(1)∵四边形ABCD是矩形，

∴AD∥BC，

∴∠ACB=∠DAC，

∵O是AC的中点，

∴AO=CO，

在△AOF和△COE中，

∴△AOF≌△COE(ASA),

∴OE=OF，且AO=CO，

∴四边形AECF是平行四边形，

又∵EF⊥AC，

∴四边形AECF是菱形；

（2）连接BD，

四边形AFCE是平行四边形

AF=CF=10

∠CDF=90°

CF=10，CD=AB=8

FD=6

AD=AF+DF=6+10=16

∠DAB=90°

==

BO=

故答案为：