题目内容
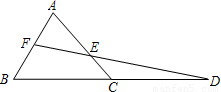
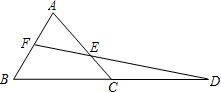 已知△ABC,延长BC到D,使CD=BC.取AB的中点F,连接FD交AC于点E.
已知△ABC,延长BC到D,使CD=BC.取AB的中点F,连接FD交AC于点E.(1)求
| AE | AC |
(2)若AB=a,FB=EC,求AC的长.
分析:(1)过点F作FM∥AC,交BC于点M.根据平行线分线段成比例定理分别找到AE,CE与FM之间的关系,得到它们的比值;
(2)结合(1)中的线段之间的关系,进行求解.
(2)结合(1)中的线段之间的关系,进行求解.
解答: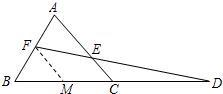 解:(1)过点F作FM∥AC,交BC于点M,
解:(1)过点F作FM∥AC,交BC于点M,
∵F为AB的中点,
∴M为BC的中点,FM=
AC.
∵FM∥AC,
∴∠CED=∠MFD,∠ECD=∠FMD.
∴△FMD∽△ECD.
∴
=
=
.
∴EC=
FM=
×
AC=
AC.
∴
=
=
=
.
(2)∵AB=a,
∴FB=
AB=
a.
∵FB=EC,
∴EC=
a.
∵EC=
AC,
∴AC=3EC=
a.
 解:(1)过点F作FM∥AC,交BC于点M,
解:(1)过点F作FM∥AC,交BC于点M,∵F为AB的中点,
∴M为BC的中点,FM=
| 1 |
| 2 |
∵FM∥AC,
∴∠CED=∠MFD,∠ECD=∠FMD.
∴△FMD∽△ECD.
∴
| DC |
| DM |
| EC |
| FM |
| 2 |
| 3 |
∴EC=
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
∴
| AE |
| AC |
| AC-EC |
| AC |
AC-
| ||
| AC |
| 2 |
| 3 |
(2)∵AB=a,
∴FB=
| 1 |
| 2 |
| 1 |
| 2 |
∵FB=EC,
∴EC=
| 1 |
| 2 |
∵EC=
| 1 |
| 3 |
∴AC=3EC=
| 3 |
| 2 |
点评:此类题要注意作平行线,能够根据平行线分线段成比例定理和相似三角形对应边成比例即可求得线段的比.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知△ABC,延长AC.
如图,已知△ABC,延长AC. 已知△ABC,延长BC到D,使CD=BC.取AB的中点F,连结FD交AC于点E.
已知△ABC,延长BC到D,使CD=BC.取AB的中点F,连结FD交AC于点E. 已知△ABC,延长BC到D,使CD=BC.取AB的中点F,连结FD交AC于点E.
已知△ABC,延长BC到D,使CD=BC.取AB的中点F,连结FD交AC于点E. 的值;
的值; 的值;
的值;