题目内容
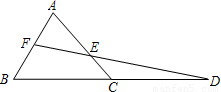
 已知△ABC,延长BC到D,使CD=BC.取AB的中点F,连结FD交AC于点E.
已知△ABC,延长BC到D,使CD=BC.取AB的中点F,连结FD交AC于点E.(1)求
| AE | AC |
(2)若AB=18,FB=EC,求AC的长.
分析:(1)如图,连接FC、AD.易证FC是△ADB的中位线,则FC
AD;然后由“平行法”证得△EFC∽△EDA,则该相似三角形的对应边成比例:
=
=2,所以由比例的性质可以求得
的值;
(2)利用(1)中的比例式,把
AB=FB=EC=9代入,即可求得AC的长度.
| ∥ |
. |
| 1 |
| 2 |
| AE |
| CE |
| AD |
| FC |
| AE |
| AC |
(2)利用(1)中的比例式,把
| 1 |
| 2 |
解答: 解:(1)如图,连接FC、AD.
解:(1)如图,连接FC、AD.
∵点F是AB的中点,CD=BC,
∴FC是△ADB的中位线,
∴FC
AD,
∴△EFC∽△EDA,
∴
=
=2,
∴
=
;
(2)∵点F是AB的中点,AB=18,FB=EC,
∴EC=
AB=9.
由(1)知,
=2,则
=2,故AE=18,
∴AC=AE+EC=18+9=27.
 解:(1)如图,连接FC、AD.
解:(1)如图,连接FC、AD.∵点F是AB的中点,CD=BC,
∴FC是△ADB的中位线,
∴FC
| ∥ |
. |
| 1 |
| 2 |
∴△EFC∽△EDA,
∴
| AE |
| CE |
| AD |
| FC |
∴
| AE |
| AC |
| 2 |
| 3 |
(2)∵点F是AB的中点,AB=18,FB=EC,
∴EC=
| 1 |
| 2 |
由(1)知,
| AE |
| CE |
| AE |
| 9 |
∴AC=AE+EC=18+9=27.
点评:本题考查了相似三角形的判定与性质.此类题要注意作平行线,能够根据相似三角形对应边成比例即可求得线段的比.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
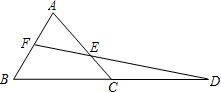 已知△ABC,延长BC到D,使CD=BC.取AB的中点F,连接FD交AC于点E.
已知△ABC,延长BC到D,使CD=BC.取AB的中点F,连接FD交AC于点E. 如图,已知△ABC,延长AC.
如图,已知△ABC,延长AC. 已知△ABC,延长BC到D,使CD=BC.取AB的中点F,连结FD交AC于点E.
已知△ABC,延长BC到D,使CD=BC.取AB的中点F,连结FD交AC于点E. 的值;
的值; 的值;
的值;