题目内容
如图,A、B是⊙O上的两点,∠AOB=120,点D是劣弧AB的切线。
(1)求证:四半AOBD是菱形;
(2)延长线段BO至点P,交⊙O于另一点C,且BP=3OB,求证:AP是⊙O的切线。

(1)证明:连接OD∵D为弧AB中点,∠AOB=120O
∴∠AOD=∠BOD =60O (1分)
又∵OA=OD=OB
∴△AOD和△BOD都是等边三角形。 (2分)
∴OA=OB=BD=DA
∴四边形AOBD是菱形 (2分)
(2)证明:连接AC
∵∠AOB=120O
∴∠AOC=60O
∴△AOC是等边三角形 (1分)
∴AC=CO (1分)
又∵BP=3OB
∴AC=PC=CO
∴△PAO为直角三角形
∴PA⊥OA
∴ PA为⊙O的切线 (2分)

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 如图,A、D是⊙O上的两个点,BC是直径,若∠D=35°,则∠OAC等于( )
如图,A、D是⊙O上的两个点,BC是直径,若∠D=35°,则∠OAC等于( )| A、65° | B、35° | C、70° | D、55° |
 如图,A、B是⊙O上的两点,AC是⊙O的切线,∠OBA=75°,⊙O的半径为1,则OC的长等于( )
如图,A、B是⊙O上的两点,AC是⊙O的切线,∠OBA=75°,⊙O的半径为1,则OC的长等于( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 20、已知:如图,E、F是AB上的两点,AE=BF,AC∥BD,∠C=∠D.求证:CF=DE.
20、已知:如图,E、F是AB上的两点,AE=BF,AC∥BD,∠C=∠D.求证:CF=DE. (2012•南京)如图,A、B是⊙O上的两个定点,P是⊙O上的动点(P不与A、B重合)、我们称∠APB是⊙O上关于点A、B的滑动角.
(2012•南京)如图,A、B是⊙O上的两个定点,P是⊙O上的动点(P不与A、B重合)、我们称∠APB是⊙O上关于点A、B的滑动角.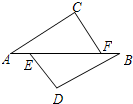 已知:如图,E、F是AB上的两点,AC=BD,AC∥BD,∠C=∠D;
已知:如图,E、F是AB上的两点,AC=BD,AC∥BD,∠C=∠D;