题目内容
若∠1+∠2=90°，∠1+∠3=90°，则∠2=∠3的理由是 ．
若∠1+∠2=180°，∠3+∠4=180°，且∠1=∠3，则∠2=∠4的理由是 ．
若∠1+∠2=180°，∠3+∠4=180°，且∠1=∠3，则∠2=∠4的理由是
考点：余角和补角
专题：
分析：（1）根据余角的性质：同角的余角相等进行解答；
（2）根据补角的性质：等角的补角相等进行解答．
（2）根据补角的性质：等角的补角相等进行解答．
解答：解：（1）∵∠1+∠2=90°，∠1+∠3=90°，
∴∠2=∠3（同角的余角相等）；
（2）∵∠1+∠2=180°，∠3+∠4=180°，∠1=∠3，
∴∠2=∠4（等角的补角相等）．
故答案为：同角的余角相等；等角的补角相等．
∴∠2=∠3（同角的余角相等）；
（2）∵∠1+∠2=180°，∠3+∠4=180°，∠1=∠3，
∴∠2=∠4（等角的补角相等）．
故答案为：同角的余角相等；等角的补角相等．
点评：此题主要考查了余角和补角，关键是掌握性质：等角的补角相等．等角的余角相等．
练习册系列答案
每课必练系列答案
相关题目
如图，在一单位长度为1cm的方格纸上，依如图所示的规律，设定点A1、A2、A3、A4、A5、A6、A7、…、An，连接点O、A1、A2组成三角形，记为△1，连接O、A2、A3组成三角形，记为△2…，连O、An、An+1组成三角形，记为△n（n为正整数），请你推断，当n为99时，△n的面积=关于x的一元二次方程（m-1）x2+x+m2-1=0的一个根为0，则m为（ ）
| A、0 | B、1 | C、-1 | D、1或-1 |
把一个平角分成三等份，两旁两个角的角平分线所成的角的度数为（ ）
| A、150° | B、120° |
| C、90° | D、60° |
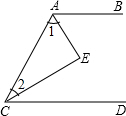如图，AE平分∠BAC，CE平分∠ACD，且AB∥CD，则∠AEC等于（ ）| A、60° | B、80° |
| C、100° | D、90° |
若式子
有意义，则x的取值范围为（ ）
| ||
| x-3 |
| A、x≥2 |
| B、x≠3 |
| C、x≤2或x≠3 |
| D、x≥2且x≠3 |