题目内容
若二次函数y=（a-1）x2+3x+a2-3a+2的图象经过原点，则a的值必为（ ）
| A、1或2 | B、0 | C、1 | D、2 |
考点：二次函数图象上点的坐标特征,解一元二次方程-因式分解法
专题：因式分解
分析：根据二次函数图象上点的坐标特征，将点（0，0）代入二次函数的解析式，列出关于a的一元二次方程，通过解方程即可求得a的值．
解答：解：∵二次函数y=（a-1）x2+3x+a2-3a+2的图象经过原点，
∴点（0，0）在二次函数y=（a-1）x2+3x+a2-3a+2的图象上，且a-1≠0，
∴a2-3a+2=0，且a-1≠0，
∴（a-1）（a-2）=0，且a-1≠0，
∴a-2=0，即a=2；
故选D．
∴点（0，0）在二次函数y=（a-1）x2+3x+a2-3a+2的图象上，且a-1≠0，
∴a2-3a+2=0，且a-1≠0，
∴（a-1）（a-2）=0，且a-1≠0，
∴a-2=0，即a=2；
故选D．
点评：本题综合考查了二次函数图象上点的坐标特征、解一元二次方程--因式分解法．注意：二次函数y=（a-1）x2+3x+a2-3a+2的自变量x的系数不为零．
练习册系列答案
相关题目
对于数x，符号[x]表示不大于x的最大整数．若[
]=3有正整数解，则正数a的取值范围是（ ）
| 3x+a |
| 2 |
| A、0＜a＜2或2＜a≤3 |
| B、0＜a＜5或6＜a≤7 |
| C、1＜a≤2或3≤a＜5 |
| D、0＜a＜2或3≤a＜5 |
如图所示的三个图形分别是等边三角形、正方形、长方形，其中AB=CD=EG，请你利用这三个图形拼接出不同立体图形展开图的示意图（至少画出四种，可以只利用其中一种图形拼接；所用图形的个数不限）．
如图中，以A，B，C，D，E，F，G，H这些点为端点的线段共有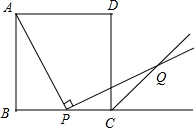
（1）如图，P是正方形ABCD的BC边上的中点，AP⊥PQ，且PQ交∠DCB的外角平分线于Q．求证：AP=PQ
如图中有四个面积相同的圆，每个圆的面积都记为S，∠ABC的两边分别经过圆心O1、O2、O3和O4，四个圆盖的面积为5（S-1），∠ABC内部被圆盖住的面积为8，阴影部分的面积为S1、S2、S3满足关系式：