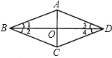
题目内容
【题目】如图,![]() 、
、![]() 两点分别位于一个池塘的两侧,池塘西南边有一座假山
两点分别位于一个池塘的两侧,池塘西南边有一座假山![]() ,在
,在![]() 的中点
的中点![]() 处有一个雕塑,小川从点
处有一个雕塑,小川从点![]() 出发,沿直线
出发,沿直线![]() 一直向前经过点
一直向前经过点![]() 走到点
走到点![]() ,并使
,并使![]() ,然后他测量点
,然后他测量点![]() 到假山
到假山![]() 的距离,则
的距离,则![]() 的长度就是
的长度就是![]() 、
、![]() 两点之间的距离.请根据题意完成下列问题:
两点之间的距离.请根据题意完成下列问题:
(1)题中给出的已知条件是什么?
已知:_______________________________________________________;
(2)得出的结论是什么?
结论:______________________________________________________;
(3)根据题意写出证明.
证明:
【答案】(1)![]() ,
,![]() 与
与![]() 相交于C,
相交于C,![]() ;(2)
;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)根据题意写出已知即可;
(2)根据全等三角形的性质写出结论即可;
(3)利用两边切夹角相等的两三角形全等,即可得出答案.
(1)已知:![]() ,
,![]() 与
与![]() 相交于C,
相交于C,![]() ;
;
(2)结论:![]() ;
;
(3)在△ECD和△ACB中,
∵ ,
,
∴△ECD≌△ACB(SAS),
∴DE=AB.

【题目】小颖和小红两位同学在学习“概率”时,做掷骰子(质地均匀的正方体)实验.
(1)他们在一次实验中共做了![]() 次试验,试验的结果如下:
次试验,试验的结果如下:
朝上的点数 |
|
|
|
|
|
|
出现的次数 |
|
|
|
|
|
|
①填空:此次实验中“![]() 点朝上”的频率为________;
点朝上”的频率为________;
②小红说:“根据实验,出现![]() 点朝上的概率最小.”她的说法正确吗?为什么?
点朝上的概率最小.”她的说法正确吗?为什么?
(2)小颖和小红在实验中如果各掷一枚骰子,那么两枚骰子朝上的点数之和为多少时的概率最大?试用列表或画树状图的方法加以说明,并求出其最大概率.
【题目】小华有一个容最为8![]() (
(![]() )的
)的![]() 盘,
盘,![]() 盘中已经存储了一个视频文件,其余空间都用来存储照片,且每张照片占用的内存容量均相同,已知剩余可用空间
盘中已经存储了一个视频文件,其余空间都用来存储照片,且每张照片占用的内存容量均相同,已知剩余可用空间![]() 与图片数量
与图片数量![]() (张)满足一次函数关系,对应数据如下表:
(张)满足一次函数关系,对应数据如下表:
图片数量 | 100 | 150 |
剩余可用空间 | 5700 | 5550 |
(1)求出![]() 与
与![]() 之间的关系式,并求出
之间的关系式,并求出![]() 盘中视频文件占用的内存容量;
盘中视频文件占用的内存容量;
(2)若![]() 盘中已经存入1280张照片,那么最多还能存入多少张照片?
盘中已经存入1280张照片,那么最多还能存入多少张照片?