Question

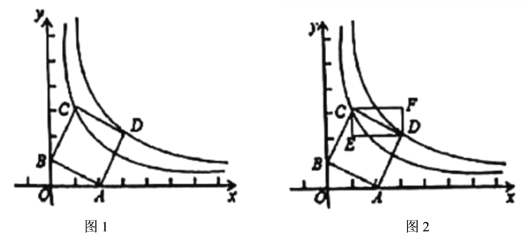
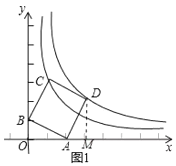
【题目】如图1，在平面直角坐标系中点，，以为顶点在第一象限内作正方形.反比例函数、分别经过、两点（1）如图2，过、两点分别作、轴的平行线得矩形，现将点沿的图象向右运动，矩形随之平移；

①试求当点落在的图象上时点的坐标_____________.

②设平移后点的横坐标为，矩形的边与，的图象均无公共点，请直接写出的取值范围____________.

Answer 1

【答案】

【解析】

（1）如图1中，作DM⊥x轴于M．利用全等三角形的性质求出点D坐标，点C坐标，得到k1 ，k2的值，设平移后点D坐标为（m，），则E（m2，），由题意：（m2）＝3，解方程即可；

（2）设平移后点D坐标为（a，），则C（a2，＋1），当点C在y＝上时，（a2）（＋1）＝6，解得a＝1＋或1（舍弃），观察图象可得结论；

解：（1）如图1中，作DM⊥x轴于M．

∵四边形ABCD是正方形，

∴AB＝AD，∠BAD＝90°，

∵∠AOB＝∠AMD＝90°，

∴∠OAB＋∠OBA＝90°，∠OAB＋∠DAM＝90°，

∴∠ABO＝∠DAM，

∴△OAB≌△MDA（AAS），

∴AM＝OB＝1，DM＝OA＝2，

∴D（3，2），

∵点D在上，

∴k2＝6，即，

同法可得C（1，3），

∵点C在上，

∴k1＝3，即，

设平移后点D坐标为（m，），则E（m2，），

由题意：（m2）＝3，

解得m＝4，

∴D（4，）；

（2）设平移后点D坐标为（a，），则C（a2，＋1），

当点C在y＝上时，（a2）（＋1）＝6，

解得a＝1＋或1（舍弃），

观察图象可知：矩形的边CE与，的图象均无公共点，

则a的取值范围为：4＜a＜1＋．