题目内容
圆O的半径为 ,E、F分别为弦AB和CD的中点,且AB⊥CD,若AB=4,CD=2
,E、F分别为弦AB和CD的中点,且AB⊥CD,若AB=4,CD=2 ,则EF的长为
,则EF的长为
- A.5
- B.

- C.

- D.

D
分析:先画草图,连接OE,OF,OB,OC,设AB与CD相交于点M,可得出四边形OEMF是矩形,再由勾股定理求得OE,OF,即可得出EF.
解答: 解:连接OE,OF,OB,OC,
解:连接OE,OF,OB,OC,
设AB与CD相交于点M,
∵E、F分别为弦AB和CD的中点,且AB⊥CD,
∴四边形OEMF是矩形,
∵AB=4,CD=2 ,
,
∴AE=BE=2,CF=DF= ,
,
∴OE2=( )2-22=2,
)2-22=2,
OF2=( )2-(
)2-( )2=3,
)2=3,
∴在Rt△OEF中,EF= =
=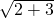 =
= .
.
故选D.
点评:本题考查了垂径定理、勾股定理以及矩形的判定,是基础知识要熟练掌握.
分析:先画草图,连接OE,OF,OB,OC,设AB与CD相交于点M,可得出四边形OEMF是矩形,再由勾股定理求得OE,OF,即可得出EF.
解答:
 解:连接OE,OF,OB,OC,
解:连接OE,OF,OB,OC,设AB与CD相交于点M,
∵E、F分别为弦AB和CD的中点,且AB⊥CD,
∴四边形OEMF是矩形,
∵AB=4,CD=2
 ,
,∴AE=BE=2,CF=DF=
 ,
,∴OE2=(
 )2-22=2,
)2-22=2,OF2=(
 )2-(
)2-( )2=3,
)2=3,∴在Rt△OEF中,EF=
 =
=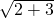 =
= .
.故选D.
点评:本题考查了垂径定理、勾股定理以及矩形的判定,是基础知识要熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,正六边形内接于圆O,圆O的半径为10,则图中阴影部分的面积为
如图,正六边形内接于圆O,圆O的半径为10,则图中阴影部分的面积为 已知Rt△ABC,
已知Rt△ABC, (2013•广安)如图,已知半径OD与弦AB互相垂直,垂足为点C,若AB=8cm,CD=3cm,则圆O的半径为( )
(2013•广安)如图,已知半径OD与弦AB互相垂直,垂足为点C,若AB=8cm,CD=3cm,则圆O的半径为( )