题目内容
【题目】在![]() 中,
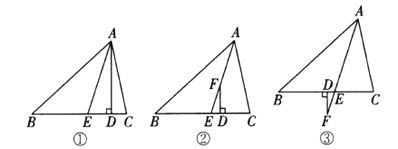
中,![]() .如图①,
.如图①,![]() 于点
于点![]() ,
,![]() 平分
平分![]() ,则易知
,则易知![]() .
.
(1)如图②,![]() 平分
平分![]() ,
, ![]() 为
为![]() 上的一点,且
上的一点,且![]() 于点
于点![]() ,这时
,这时![]() 与
与![]() 、
、![]() 有何数量关系?请说明理由;
有何数量关系?请说明理由;
(2)如图③,![]() 平分
平分![]() ,
,![]() 为
为![]() 延长线上的一点,
延长线上的一点,![]() 于点
于点![]() ,请你写出这时
,请你写出这时![]() 与
与![]() 、
、![]() 之间的数量关系(只写结论,不必说明理由).
之间的数量关系(只写结论,不必说明理由).
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)由角平分线的性质和三角形的内角和得出∠BAE=90°-![]() (∠C+∠B),外角的性质得出∠AEC=90°+
(∠C+∠B),外角的性质得出∠AEC=90°+![]() (∠B-∠C),在△EFD中,由三角形内角和定理可得∠EFD;
(∠B-∠C),在△EFD中,由三角形内角和定理可得∠EFD;
(2)由角平分线的性质和三角形的内角和得出∠BAE=90°-![]() (∠C+∠B), 外角的性质得出∠DEF=90°+
(∠C+∠B), 外角的性质得出∠DEF=90°+![]() (∠B-∠C), 在△EFD中,由三角形内角和定理可得∠EFD;
(∠B-∠C), 在△EFD中,由三角形内角和定理可得∠EFD;
试题解析:
∠EFD=![]() (∠C-∠B),理由如下:
(∠C-∠B),理由如下:
∵AE平分∠BAC,
∴∠BAE=![]() =90°-
=90°-![]() (∠C+∠B),
(∠C+∠B),
∵∠AEC为△ABE的外角,
∴∠AEC=∠B+90°-![]() (∠C+∠B)=90°+
(∠C+∠B)=90°+![]() (∠B-∠C),
(∠B-∠C),
∵FD⊥BC,
∴∠FDE=90°.
∴∠EFD=90°-90°-![]() (∠B-∠C)
(∠B-∠C)
∴∠EFD=![]() (∠C-∠B).
(∠C-∠B).
(2)∠EFD=![]() (∠C-∠B),理由如下:
(∠C-∠B),理由如下:
∵AE平分∠BAC,
∴∠BAE=![]() .
.
∵∠DEF为△ABE的外角,
∴∠DEF=∠B+![]() =90°+
=90°+![]() (∠B-∠C),
(∠B-∠C),
∵FD⊥BC,
∴∠FDE=90°.
∴∠EFD=90°-90°-![]() (∠B-∠C),
(∠B-∠C),
∴∠EFD=![]() (∠C-∠B).
(∠C-∠B).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目