Question

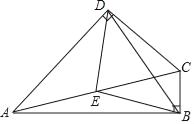
【题目】已知：如图，在四边形ABCD中，∠ABC=∠ADC=90°，点E是AC的中点．（1）求证：△BED是等腰三角形：

（2）当∠BCD=_____°时，△BED是等边三角形．

Answer 1

【答案】150

【解析】整体分析：

(1)根据直角三角形斜边上的中线等于斜边的一半，即可求证；(2)由△BED是等边三角形，可得∠BAD=30°，从而在四边形ABCD中，由内角和定理可得∠BCD的度数.

证明：（1）∵∠ABC=∠ADC=90°，点E是AC边的中点，

∴BE=AC，DE=AC，

∴BE=DE，

∴△BED是等腰三角形；

（2）∵AE=ED，

∴∠DAE=∠EDA，

∵AE=BE，

∴∠EAB=∠EBA，

∵∠DAE+∠EDA=∠DEC，

∠EAB+∠EBA=∠BEC，

∴∠DAB=∠DEB，

∵△BED是等边三角形，

∴∠DEB=60°，

∴∠BAD=30°，

∴∠BCD=360°﹣90°﹣90°﹣30°=150°．

故答案为150．