题目内容
 在△ABC中,∠ABC的外角平分线和∠ACB的外角平分线交于点O,求:∠O与∠BAC的关系.
在△ABC中,∠ABC的外角平分线和∠ACB的外角平分线交于点O,求:∠O与∠BAC的关系.考点:三角形内角和定理,三角形的外角性质
专题:
分析:先根据角平分线的定义得∠1=∠2,∠4=∠5,根据外角的性质得∠1+∠2=∠A+∠6,∠4+∠5=∠3+∠A,再由∠1+∠2+∠3=180°,∠4+∠5+∠6=180°,∠O+∠2+∠5=180°,可得出答案.
解答: 解:如图,
解:如图,
∵BO、CO分别平分∠ABC和∠ACB的外角,
∴∠1=∠2,∠4=∠5,
∵∠1+∠2=∠A+∠6,∠4+∠5=∠3+∠A,
即2∠2+∠3=180°①,2∠5+∠6=180°②,
∴①+②得2∠2+2∠5+∠3+∠6=360°③,
∵∠O+∠2+∠5=180°④,
∴360°-2∠O+∠3+∠6=360°,
∵∠6+∠3=180°-∠A,
∴180°-∠A-2∠O=0,
∴∠A+2∠O=180°.
 解:如图,
解:如图,∵BO、CO分别平分∠ABC和∠ACB的外角,
∴∠1=∠2,∠4=∠5,
∵∠1+∠2=∠A+∠6,∠4+∠5=∠3+∠A,
即2∠2+∠3=180°①,2∠5+∠6=180°②,
∴①+②得2∠2+2∠5+∠3+∠6=360°③,
∵∠O+∠2+∠5=180°④,
∴360°-2∠O+∠3+∠6=360°,
∵∠6+∠3=180°-∠A,
∴180°-∠A-2∠O=0,
∴∠A+2∠O=180°.
点评:本题考查了三角形的内角和定理,三角形外角的性质,是基础知识,但是这个题比较繁琐.

练习册系列答案
相关题目
 如图,8×8的正方形网格中,每个小正方形的边长为1个长度单位,点B的坐标为(1,1)点A的坐标为(3,-2)
如图,8×8的正方形网格中,每个小正方形的边长为1个长度单位,点B的坐标为(1,1)点A的坐标为(3,-2)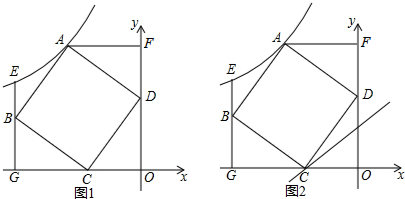
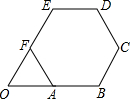 如图,正六边形ABCDEF的边长为2
如图,正六边形ABCDEF的边长为2