题目内容
1. 如图,在平面直角坐标系中,点A(0,a),点B(b,0),点D(d,0),其中a、b、d满足|a-3|+$\sqrt{b+1}$+(2-d)2=0,DE⊥x轴,且∠BED=∠ABO,直线AE交x轴于点C.
如图,在平面直角坐标系中,点A(0,a),点B(b,0),点D(d,0),其中a、b、d满足|a-3|+$\sqrt{b+1}$+(2-d)2=0,DE⊥x轴,且∠BED=∠ABO,直线AE交x轴于点C.(1)求A、B、D三点的坐标;
(2)求证:△ABO≌△BED;
(3)求直线AE的解析式;
(4)动点P在y轴上,求PE+PC取最小值时点P的坐标.
分析 (1)根据非负数的性质,几个非负数的和等于0,则每个数是0即可列方程求得a、b、d的值,从而求解;
(2)根据(1)即可求得OA和BD的长,然后利用AAS即可证得;
(3)根据(2)求得DE的长,则E的坐标即可求得,然后利用待定系数法求得AE的解析式;
(3)首先求得C的坐标,然后求得C关于y轴的对称点,这个点与E所在的直线与y轴的交点就是P,首先求得直线解析式,然后求P的坐标即可.
解答 解:(1)根据题意得:a-3=0,b+1=0,2-d=0,
解得:a=3,b=-1,c=2,
则A的坐标是(0,3),B的坐标是(-1,0),D的坐标是(2,0);
(2)∵B的坐标是(-1,0),D的坐标是(2,0),A的坐标是(0,3),
∴BD=3,AO=3,
∴BD=AO,
在△ABO和△BED中,
$\left\{\begin{array}{l}{∠BED=∠ABO}\\{∠AOB=∠BDE}\\{AO=BD}\end{array}\right.$,
∴△ABO≌△BED;
(3)由(2)得E(2,1),
设AE的解析式是y=kx+b,
根据题意得:$\left\{\begin{array}{l}{b=3}\\{2k+b=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$
则AE的解析式是:y=-x+3;
(4)在y=-x+3中,令y=0,解得:x=3,
则C的坐标是(3,0),则C关于y轴对称点(-3,0).
设经过(-3,0)和E的直线解析式是y=mx+n,
则$\left\{\begin{array}{l}{-3m+n=0}\\{2m+n=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=\frac{1}{5}}\\{n=\frac{3}{5}}\end{array}\right.$.
则解析式是y=$\frac{1}{5}$x+$\frac{3}{5}$,
令x=0,解得y=$\frac{3}{5}$.
则P的坐标是(0,$\frac{3}{5}$).
点评 本题考查了待定系数法求直线的解析式,以及图形的对称以及全等三角形的判定和性质,正确确定P的位置是关键.

| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
 实数a、b、c在数轴上的对应点如图所示,化简$|{b-a}|+\sqrt{{{({b-c})}^2}}-\sqrt{a^2}$.
实数a、b、c在数轴上的对应点如图所示,化简$|{b-a}|+\sqrt{{{({b-c})}^2}}-\sqrt{a^2}$.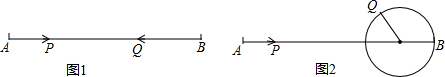
 如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,△ABC面积是28cm2,AB=16cm,AC=12cm,则DE的长为( )
如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,△ABC面积是28cm2,AB=16cm,AC=12cm,则DE的长为( )