题目内容
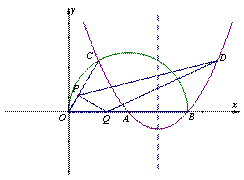
如图,在平面直角坐标系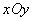 中,半圆的圆心点A在
中,半圆的圆心点A在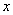 轴上,直径OB=8,点C是半圆上一点,
轴上,直径OB=8,点C是半圆上一点,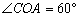 ,二次函数
,二次函数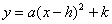 的图象经过点A、B、C.动点P和点Q同时从点O出发,点P以每秒1个单位的速度从O点运动到点C,点Q以每秒两个单位的速度在OB上运动,当点P运动到点C时,点Q随之停止运动.点D是点C关于二次函数图象对称轴的对称点,顺次连接点D、P、Q,设点P的运动时间
的图象经过点A、B、C.动点P和点Q同时从点O出发,点P以每秒1个单位的速度从O点运动到点C,点Q以每秒两个单位的速度在OB上运动,当点P运动到点C时,点Q随之停止运动.点D是点C关于二次函数图象对称轴的对称点,顺次连接点D、P、Q,设点P的运动时间 为t秒,△DPQ的面积为y.
为t秒,△DPQ的面积为y.
(1)求二次函数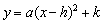 的表达式;
的表达式;
(2)当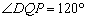 时,直接写出点P的坐标;
时,直接写出点P的坐标;
(3)在点P和点Q运动的过程中,△DPQ的面积存在最大值吗?如果存在,请求出此时的t值和△DPQ面积的最大值;如果不存在,请说明理由.
 |  |
 (1)解:连接AC
(1)解:连接AC
 为半圆的圆心,OB=8
为半圆的圆心,OB=8



 △AOC为等边三角形
△AOC为等边三角形


易知
 二次函数图象的对称轴为x=6
二次函数图象的对称轴为x=6
将点 ,
, 分别代入
分别代入 解得:
解得:
 .
.
(2)
(3)连接BC、 DB,延长DB、PQ交于点E

 ,
,



 △OPQ∽△OCB
△OPQ∽△OCB
 ∠OPQ=∠OCB
∠OPQ=∠OCB
 为半圆的直径
为半圆的直径
 ∠OCB=90º
∠OCB=90º
 ∠OPQ=90º
∠OPQ=90º
在Rt△OPQ中,PQ=
连接CD
 点D是点C关于二次函数图象对称轴的对称点
点D是点C关于二次函数图象对称轴的对称点
 CD∥OB
CD∥OB

 且对称轴为x=6
且对称轴为x=6


 CD=OB=8
CD=OB=8
 四边形OCDB为平行四边形
四边形OCDB为平行四边形
 O
O C∥DB
C∥DB
 ∠DEP=∠OPQ=90º
∠DEP=∠OPQ=90º
在Rt△BEQ中,∠BQE= 30º,
30º,



 S△DPQ=
S△DPQ=
即
 当t =4时,△DPQ的面积的最大值为
当t =4时,△DPQ的面积的最大值为  .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 中,
中, ,以
,以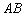 为直径作⊙
为直径作⊙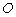 ,交
,交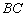 于点
于点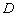 ,连接
,连接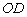 ,过点
,过点 ,交
,交 于点
于点 。
。 ;
; ,
, 时,求
时,求 及
及 的长。
的长。

 是△
是△ 的外接圆,
的外接圆, ,连结
,连结 并延长交⊙
并延长交⊙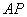 于点
于点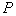 .
. ;
; (2)若
(2)若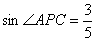 ,
,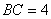 ,求
,求