题目内容
 如图,在等腰梯形ABCD中,AD∥BC,AE⊥BC于E,AD=6,BC=14,AE=
如图,在等腰梯形ABCD中,AD∥BC,AE⊥BC于E,AD=6,BC=14,AE= ,点F在DC上运动,连接EF、AF.
,点F在DC上运动,连接EF、AF.
(1)求∠B的度数.
(2)设FC=x,△FEC的面积为y,用含x的代数式表示y.
(3)当△FEC的面积为等腰梯形面积的 时,判断AF与EF的大小关系,并证明你的结论.
时,判断AF与EF的大小关系,并证明你的结论.
解:(1)
过D作DM⊥BC于M,
∵AE⊥BC,
∴∠AEM=∠AEB=∠DMC=∠DME=90°,AE∥DM,
∵AD∥BC,
∴四边形AEMD是矩形,
∴AE=DM,
∵AB=DC,
∴在Rt△AEB和Rt△DMC中,由勾股定理得:BE=CM= (BC-AD)=
(BC-AD)= ×(14-6)=4,
×(14-6)=4,
在Rt△AEB中,tanB= =
= =
= ,
,
∴∠B=60°.
(2)
过E作EN⊥CD于N,
则∠ENC=90°,CE=14-4=10,
∵四边形ABCD是等腰梯形,
∴∠C=∠B=60°,
∴∠CEN=30°,
∴CN= CE=5,由勾股定理得:EN=
CE=5,由勾股定理得:EN=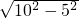 =5
=5 ,
,
即y= CF•EN=
CF•EN= x•5
x•5 ,
,
∴y= x.
x.
(3)AF=EF,
证明:梯形ABCD的面积是 ×(AD+BC)×AE=
×(AD+BC)×AE= (6+14)×4
(6+14)×4 =40
=40 ,
,
∵△FEC的面积为等腰梯形面积的 ,
,
∴y= x=
x= ×40
×40 ,
,
解得:x=4,
即CF=4,
∵在Rt△ABE中,由勾股定理得:AB=DC= =8,
=8,
∴F为CD中点,
过F作FQ∥AD,交AE于Q,
∵AD∥BC,
∴AD∥FQ∥BC,
∴AQ=EQ,
∵AE⊥BC,
∴FQ⊥AE,
∴AF=EF.
分析:(1)过D作DM⊥BC于M,求出BE=CM,求出BE值,解直角三角形即可求出答案.
(2)过E作EN⊥CD于N,求出CE,解直角三角形求出EN,根据三角形面积公式求出即可.
(3)根据面积得出关于x的方程,求出CF,过F作FQ∥AD,交AE于Q,求出Q为AE中点,FQ⊥AE,根据线段垂直平分线求出即可.
点评:本题考查了等腰梯形性质,矩形的性质和判定,勾股定理,一次函数的解析式,平行线等分线段定理,线段垂直平分线性质,三角形的面积的应用,综合性比强,有一定的难度.

过D作DM⊥BC于M,
∵AE⊥BC,
∴∠AEM=∠AEB=∠DMC=∠DME=90°,AE∥DM,
∵AD∥BC,
∴四边形AEMD是矩形,
∴AE=DM,
∵AB=DC,
∴在Rt△AEB和Rt△DMC中,由勾股定理得:BE=CM=
 (BC-AD)=
(BC-AD)= ×(14-6)=4,
×(14-6)=4,在Rt△AEB中,tanB=
 =
= =
= ,
,∴∠B=60°.
(2)

过E作EN⊥CD于N,
则∠ENC=90°,CE=14-4=10,
∵四边形ABCD是等腰梯形,
∴∠C=∠B=60°,
∴∠CEN=30°,
∴CN=
 CE=5,由勾股定理得:EN=
CE=5,由勾股定理得:EN=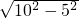 =5
=5 ,
,即y=
 CF•EN=
CF•EN= x•5
x•5 ,
,∴y=
 x.
x.(3)AF=EF,
证明:梯形ABCD的面积是
 ×(AD+BC)×AE=
×(AD+BC)×AE= (6+14)×4
(6+14)×4 =40
=40 ,
,∵△FEC的面积为等腰梯形面积的
 ,
,∴y=
 x=
x= ×40
×40 ,
,解得:x=4,
即CF=4,
∵在Rt△ABE中,由勾股定理得:AB=DC=
 =8,
=8,∴F为CD中点,
过F作FQ∥AD,交AE于Q,

∵AD∥BC,
∴AD∥FQ∥BC,
∴AQ=EQ,
∵AE⊥BC,
∴FQ⊥AE,
∴AF=EF.
分析:(1)过D作DM⊥BC于M,求出BE=CM,求出BE值,解直角三角形即可求出答案.
(2)过E作EN⊥CD于N,求出CE,解直角三角形求出EN,根据三角形面积公式求出即可.
(3)根据面积得出关于x的方程,求出CF,过F作FQ∥AD,交AE于Q,求出Q为AE中点,FQ⊥AE,根据线段垂直平分线求出即可.
点评:本题考查了等腰梯形性质,矩形的性质和判定,勾股定理,一次函数的解析式,平行线等分线段定理,线段垂直平分线性质,三角形的面积的应用,综合性比强,有一定的难度.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 在,求出这样的t的值;若不存在,请说明理由.
在,求出这样的t的值;若不存在,请说明理由. 10、如图,在等腰梯形ABCD中,AD∥BC,AB=DC,E为AD的中点,求证:BE=CE.
10、如图,在等腰梯形ABCD中,AD∥BC,AB=DC,E为AD的中点,求证:BE=CE. 已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E、F分别在AB、DC上,且BE=3EA,CF=3FD.
已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E、F分别在AB、DC上,且BE=3EA,CF=3FD. (2012•广州)如图,在等腰梯形ABCD中,BC∥AD,AD=5,DC=4,DE∥AB交BC于点E,且EC=3,则梯形ABCD的周长是( )
(2012•广州)如图,在等腰梯形ABCD中,BC∥AD,AD=5,DC=4,DE∥AB交BC于点E,且EC=3,则梯形ABCD的周长是( )
