题目内容
2. 二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx+m=0有实数根,则m的最大值为3.
二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx+m=0有实数根,则m的最大值为3.
分析 先根据抛物线的开口向上可知a>0,由顶点纵坐标为-3得出b与a关系,再根据一元二次方程ax2+bx+m=0有实数根可得到关于m的不等式,求出m的取值范围即可.
解答 方法一解:∵抛物线的开口向上,顶点纵坐标为-3,
∴a>0.
-$\frac{{b}^{2}}{4a}$=-3,即b2=12a,
∵一元二次方程ax2+bx+m=0有实数根,
∴△=b2-4am≥0,即12a-4am≥0,即12-4m≥0,解得m≤3,
∴m的最大值为3,
方法二:解:一元二次方程ax2+bx+m=0有实数根,则二次函数y=ax2+bx的图象与直线y=-m有交点,
由图象得,-m≥-3,解得m≤3,
∴m的最大值为3,
故答案为3.
点评 本题考查的是抛物线与x轴的交点,根据题意判断出a的符号及a、b的关系是解答此题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
17.下列四个实数中,绝对值最大的数是( )
| A. | -$\sqrt{20}$ | B. | $\sqrt{15}$ | C. | $\root{3}{19}$ | D. | -$\root{3}{62}$ |
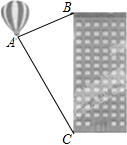 如图,据热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,求这栋高楼BC的高度.
如图,据热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,求这栋高楼BC的高度.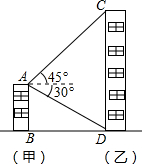 如图,甲楼AB的高度为21m,在甲楼楼顶A处测得乙楼顶端C处的仰角为45°,测得乙楼底部D处的俯角为30°.求乙楼CD的高度(结果精确到0.1米,$\sqrt{3}$≈1.73,$\sqrt{2}$,1.41)
如图,甲楼AB的高度为21m,在甲楼楼顶A处测得乙楼顶端C处的仰角为45°,测得乙楼底部D处的俯角为30°.求乙楼CD的高度(结果精确到0.1米,$\sqrt{3}$≈1.73,$\sqrt{2}$,1.41) 如图,直线AB、CD相交于点0,OE平分∠AOD,∠FOC=96°,∠BOF=40°,试求∠AOE的度数.
如图,直线AB、CD相交于点0,OE平分∠AOD,∠FOC=96°,∠BOF=40°,试求∠AOE的度数.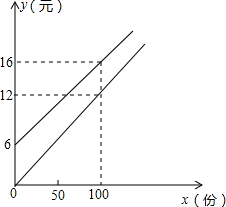 我校实行学案教学,需印刷若干份数学学案.印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示:
我校实行学案教学,需印刷若干份数学学案.印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示: 某人骑自行车从A地出发,沿正东方向前进至B处后,右转15°,沿直线向前驶到C处,这时他想仍按正东方向行驶,那么他转的方向和角度是向左方向转15度.
某人骑自行车从A地出发,沿正东方向前进至B处后,右转15°,沿直线向前驶到C处,这时他想仍按正东方向行驶,那么他转的方向和角度是向左方向转15度.