题目内容
3.如果最简根式$\sqrt{2015-2n}$与$\sqrt{6n+15}$能够合并,那么n=250.分析 根据同类二次根式的概念,可得关于n的方程,根据解方程,可得答案.
解答 解:由最简根式$\sqrt{2015-2n}$与$\sqrt{6n+15}$能够合并,得
2015-2n=6n+15.
解得n=250,
故答案为:250.
点评 本题考查同类二次根式的概念,同类二次根式是化为最简二次根式后,被开方数相同的二次根式称为同类二次根式.

练习册系列答案
相关题目
8. 如图,直线AB∥CD,AF交CD于点E,∠CEF=135°,则∠A等于( )
如图,直线AB∥CD,AF交CD于点E,∠CEF=135°,则∠A等于( )
 如图,直线AB∥CD,AF交CD于点E,∠CEF=135°,则∠A等于( )
如图,直线AB∥CD,AF交CD于点E,∠CEF=135°,则∠A等于( )| A. | 35° | B. | 40° | C. | 45° | D. | 50° |
13.-5的相反数是( )
| A. | $-\frac{1}{5}$ | B. | $\frac{1}{5}$ | C. | -5 | D. | 5 |
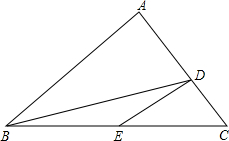 如图,在△ABC中,D、E分别是AC、BC边上的一点,AD=2DC,BE=EC,若△DBE的面积为1,则△ABC的面积等于( )
如图,在△ABC中,D、E分别是AC、BC边上的一点,AD=2DC,BE=EC,若△DBE的面积为1,则△ABC的面积等于( )