题目内容
15.(1)计算:-2-2×$\sqrt{8}$+|1-$\sqrt{2}$|+6cos45°+1(2)解不等式组$\left\{\begin{array}{l}{\frac{x-3}{2}+3≥x+1}\\{1-3(x-1)<8-x}\end{array}\right.$并写出该不等式组的整数解.
分析 (1)本题涉及负整数指数幂、绝对值、特殊角的三角函数值、二次根式化简四个考点.针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果;
(2)首先把两个不等式的解集分别解出来,再根据大大取大,小小取小,比大的小比小的大取中间,比大的大比小的小无解的原则,求得不等式的解集,再求其整数解.
解答 解:(1)-2-2×$\sqrt{8}$+|1-$\sqrt{2}$|+6cos45°+1
=-$\frac{1}{4}$×2$\sqrt{2}$+$\sqrt{2}$-1+6×$\frac{\sqrt{2}}{2}$+1
=-$\frac{\sqrt{2}}{2}$+$\sqrt{2}$-1+3$\sqrt{2}$+1
=$\frac{7\sqrt{2}}{2}$;
(2)由$\frac{x-3}{2}$+3≥x+1得x≤1,
由1-3(x-1)<8-x得x>-2,
所以-2<x≤1,则不等式组的整数解为-1,0,1.
点评 本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟记特殊角的三角函数值,熟练掌握负整数指数幂、二次根式、绝对值等考点的运算.同时考查不等式组的解集,以及在这个范围内的整数解.

练习册系列答案
相关题目
5.在Rt△ABC中,∠C=90°,AB=3,AC=2,则cosA的值是( )
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{5}}{3}$ |
7.下列问题中,是正比例函数的关系的是( )
| A. | 矩形面积一定,长与宽的关系 | |
| B. | 正方形面积和边长的关系 | |
| C. | 三角形面积一定,底边和底边上的高的关系 | |
| D. | 匀速运动中,速度固定时,路程和时间的关系 |
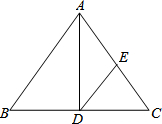 如图,已知在△ABC中,AB=AC,AD是BC边上的高线,DE∥AB交AC于点E,试找出图中所有的等腰三角形(△ABC除外),并对其中的一个等腰三角形加以说明.
如图,已知在△ABC中,AB=AC,AD是BC边上的高线,DE∥AB交AC于点E,试找出图中所有的等腰三角形(△ABC除外),并对其中的一个等腰三角形加以说明.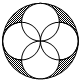 如图,四个半径为1的小圆都过大圆圆心且与大圆相内切,则阴影部分的面积为2π-4.
如图,四个半径为1的小圆都过大圆圆心且与大圆相内切,则阴影部分的面积为2π-4.