题目内容
7．已知1+a+a2+a3=0，求a+a2+a3+a4+…+a2016的值．分析 首先将a+a2+a3+…+a2016变形为：a（a+a2+a3）+a5（1+a+a2+a3）…+a2013（1+a+a2+a3），然后将a3+a2+a+1=0代入即可求得答案．
解答 解：∵a3+a2+a+1=0，
∴a+a2+a3+…+a2016
=a（1+a+a2+a3）+a5（1+a+a2+a3）…+a2013（1+a+a2+a3）
=0．
点评 此题考查了因式分解的应用，分组分解与整体代入是求得答案的关键．
练习册系列答案
阅读快车系列答案
相关题目
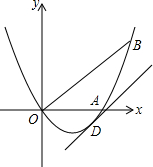如图，已知抛物线y=ax2+bx（a≠0）经过A（3，0），B（4，4）两点．
如图所示，东西和南北街道交于点O，甲沿东西道由西向东走，速度是每秒4m，乙沿南北道由南向北走，速度是每秒3m，当乙通过O点后又继续前进50m时，甲刚好通过O点，当甲、乙相距85m时，求每个人的位置．
如图，HI∥BJ，JI∥BH，求证：△BIH≌△IBJ．