题目内容
在各个内角都相等的多边形中,一个外角比一个内角少120°,求这个多边形的一个内角的度数和它的边数.
【考点】多边形内角与外角.
【分析】一个多边形的每个内角都相等,一个外角比一个内角少120°,又由于内角与外角的和是180度.设外角是x,则内角是120°+x,列方程求解即可.
【解答】解:设外角是x,则内角是120°+x,依题意有
x+120°+x=180°,
解得x=30°,
120°+x=150°,
而任何多边形的外角是360°,
则多边形中外角的个数是360÷30=12,
故这个多边形的边数是12,每个内角的度数是150°.
【点评】本题考查了多边形内角与外角,根据多边形的内角与外角的关系转化为方程的问题,并利用了多边形的外角和定理;已知外角求边数的这种方法是需要熟记的内容.

练习册系列答案
相关题目





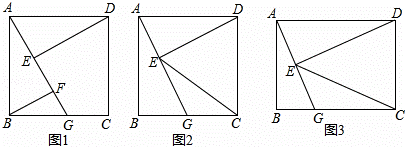
 BG,求
BG,求 ;
;