Question

7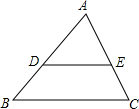．如图所示，在△ABC中，$\frac{AD}{DB}$=$\frac{AE}{EC}$，AB=12，AE=6，EC=4．
（1）求AD的长；
（2）试说明$\frac{DB}{AB}=\frac{EC}{AC}$成立．

Answer 1

分析 （1）利用$\frac{AD}{DB}$=$\frac{AE}{EC}$和比例性质和直接计算出AD；
（2）根据比例的性质由$\frac{AD}{DB}$=$\frac{AE}{EC}$得到$\frac{AB}{DB}$=$\frac{AC}{EC}$，然后再利用比例性质即可得到$\frac{DB}{AB}=\frac{EC}{AC}$．

解答 解：（1）∵$\frac{AD}{DB}$=$\frac{AE}{EC}$，
∴$\frac{AD}{12-AD}$=$\frac{6}{4}$，
∴AD=$\frac{36}{5}$；
（2）∵$\frac{AD}{DB}$=$\frac{AE}{EC}$，
∴$\frac{AD+DB}{DB}$=$\frac{EC+AE}{EC}$，即$\frac{AB}{DB}$=$\frac{AC}{EC}$，
∴$\frac{DB}{AB}=\frac{EC}{AC}$．

点评 本题考查了平行线分线段成比例：三条平行线截两条直线，所得的对应线段成比例．也考查了比例的性质．