题目内容
 已知△ABC和△BDE都是等边三角形.则下列结论:
已知△ABC和△BDE都是等边三角形.则下列结论:(1)AE=CD;(2)BF=BG;(3)HB平分∠AHD;(4)∠AHC=60°;(5)△BFG是等边三角形;(6)FG∥AD
其中正确的有
考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:
分析:由题中条件可得△ABE≌△CBD,得出对应边、对应角相等,进而得出△BGD≌△BFE,△ABF≌△CGB,再由边角关系即可求解题中结论是否正确,进而可得出结论.
解答:解:∵△ABC与△BDE为等边三角形,
∴AB=BC,BD=BE,∠ABC=∠DBE=60°,
∴∠ABE=∠CBD,
在△ABE和△CBD中,
,
∴△ABE≌△CBD(SAS),
∴AE=CD,∠BDC=∠AEB,
又∵∠DBG=∠FBE=60°,
在△BGD和△BFE中,
∴△BGD≌△BFE(ASA),
∴BG=BF,∠BFG=∠BGF=60°,
∴△BFG是等边三角形,
∴FG∥AD,
∵BF=BG,AB=BC,∠ABF=∠CBG=60°,
在△ABF和△CGB中,
,
∴△ABF≌△CGB(SAS),
∴∠BAF=∠BCG,
∴∠CAF+∠ACB+∠BCD=∠CAF+∠ACB+∠BAF=60°+60°=120°,
∴∠AHC=60°,
∵∠FHG+∠FBG=120°+60°=180°,
∴B、G、H、F四点共圆,
∵FB=GB,
∴∠FHB=∠GHB,
∴BH平分∠GHF,
∴题中①②③④⑤⑥都正确.
故答案为:①②③④⑤⑥.
∴AB=BC,BD=BE,∠ABC=∠DBE=60°,
∴∠ABE=∠CBD,
在△ABE和△CBD中,
|
∴△ABE≌△CBD(SAS),
∴AE=CD,∠BDC=∠AEB,
又∵∠DBG=∠FBE=60°,
在△BGD和△BFE中,
|
∴△BGD≌△BFE(ASA),
∴BG=BF,∠BFG=∠BGF=60°,
∴△BFG是等边三角形,
∴FG∥AD,
∵BF=BG,AB=BC,∠ABF=∠CBG=60°,
在△ABF和△CGB中,
|
∴△ABF≌△CGB(SAS),
∴∠BAF=∠BCG,
∴∠CAF+∠ACB+∠BCD=∠CAF+∠ACB+∠BAF=60°+60°=120°,
∴∠AHC=60°,
∵∠FHG+∠FBG=120°+60°=180°,
∴B、G、H、F四点共圆,
∵FB=GB,
∴∠FHB=∠GHB,
∴BH平分∠GHF,
∴题中①②③④⑤⑥都正确.
故答案为:①②③④⑤⑥.
点评:本题主要考查了等边三角形的性质及全等三角形的判定及性质问题,能够熟练掌握等边三角形的各种判定方法和全等三角形的判定方法是解题的关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
在函数y=
中,自变量x的取值范围是( )
| x-3 |
| A、x>0 | B、x≥0 |
| C、x>3 | D、x≥3 |
 图中几何体的主视图是( )
图中几何体的主视图是( )A、 |
B、 |
C、 |
D、 |
 如图,在平面直角坐标系中有一个6×2的矩形DEFG网格,每个小正方形的边长都是1个单位长度,函数y=
如图,在平面直角坐标系中有一个6×2的矩形DEFG网格,每个小正方形的边长都是1个单位长度,函数y=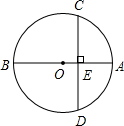 已知,AB为⊙O的直径,弦CD⊥AB,E为垂足.若BE=6,AE=4,则CD=
已知,AB为⊙O的直径,弦CD⊥AB,E为垂足.若BE=6,AE=4,则CD= 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列五个结论中:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列五个结论中: