题目内容
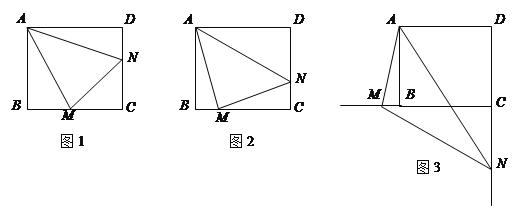
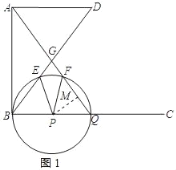
【题目】如图，AD∥BC，∠ABC＝90°，AD＝3，AB＝4，点P为射线BC上一动点，以P为圆心，BP长为半径作⊙P，交射线BC于点Q，联结BD、AQ相交于点G，⊙P与线段BD、AQ分别相交于点E、F．
（1）如果BE＝FQ，求⊙P的半径；
（2）设BP＝x，FQ＝y，求y关于x的函数关系式，并写出x的取值范围；
（3）联结PE、PF，如果四边形EGFP是梯形，求BE的长．
【答案】（1）⊙P的半径为
；（2）x的取值范围为
；（3）BE＝
或
．
【解析】
（1）由题意BE＝FQ可得∠BPE＝∠FPQ，进而可得∠EBP＝∠FQP.又AD∥BC，故∠ADB＝∠EBP，即∠FQP＝∠ADB，故两角的正切值相等即可求出半径.
（2）要求y关于x的函数关系式即可通过过P点做垂线PM，将QM用含x的式子表示，利用QM＝PQcos∠AQB＝
，而FQ=2QM，即
；根据题意圆与D点相交时，x最大，可求出x的取值范围；
（3）根据题意四边形EGFP是梯形，由于P点是动点所以产生两种情况，当GF∥EP时和GE∥FP时，故应进行分类讨论.①当GF∥EP时，可发现PE为△BGQ的中点，根据线段关系可求得BP的长度，因为△BGQ和△DGA相似，故有
，可求得BG＝
，所以BE=
BG.②当GE∥FP时，过点P作PN⊥BG ，跟①同理，可求得BE＝2BN.
（1）∵BE＝FQ，
∴∠BPE＝∠FPQ，
∵PE＝PB，
∴∠EBP＝（180°﹣∠EPB），
同理∠FQP＝（180°﹣∠FPQ），
∴∠EBP＝∠FQP，
∵AD∥BC，
∴∠ADB＝∠EBP，
∴∠FQP＝∠ADB，
∴tan∠FQP＝tan∠ADB＝
，
设⊙P的半径为r，则tan∠FQP＝
，
∴
，
解得：r＝，
∴⊙P的半径为；
（2）过点P作PM⊥FQ，垂足为点M，如图1所示：
在Rt△ABQ中，cos∠AQB＝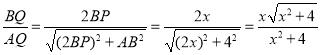
，
在Rt△PQM中，QM＝PQcos∠AQB＝，
∵PM⊥FQ，PF＝PQ，
∴FQ＝2QM＝
，
∴，
当圆与D点相交时，x最大，作DH⊥BC于H，如图2所示：
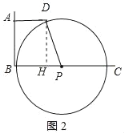
则PD＝PB＝x，DH＝AB＝4，BH＝AD＝3，
则PH＝BP﹣BH＝x﹣3，
在Rt△PDH中，由勾股定理得：42+（x﹣3）2＝x2，
解得：x＝
，
∴x的取值范围为：0＜x≤；
（3）设BP＝x，分两种情况：
①EP∥AQ时，
∴∠BEP＝∠BGQ，
∵PB＝PE，
∴∠PBE＝∠BEP，
∴∠BGQ＝∠PBE，
∴QG＝QB＝2x，
同理：AG＝AD＝3，
在Rt△ABQ中，由勾股定理得：42+（2x）2＝（3+2x）2，
解得：x＝
，
∴QG＝QB＝2x＝
，
∵EP∥AQ，PB＝PQ，
∴BE＝EG，
∵AD∥BC，
∴，
即
，
解得：BG＝，
∴BE＝BG＝；
②PF∥BD时，同①得：BG＝BQ＝2x，DG＝AD＝3，
在Rt△ABD中，由勾股定理得：42+32＝（3+2x）2，
解得：x＝1或x＝﹣4（舍去），
∴BQ＝2，
∴BP＝1，
作PN⊥BG于N，则BE＝2BN，如图3所示：
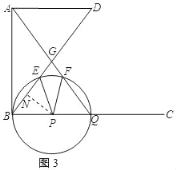
∵AD∥BC，
∴∠PBN＝∠ADB，
∴cos∠PBN＝cos∠ADB＝
，即
＝，
∴BN＝，
∴BE＝2BN＝；
综上所述，BE=或．
