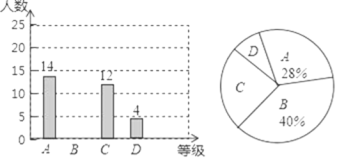
题目内容
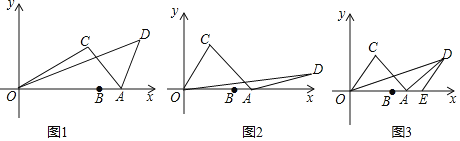
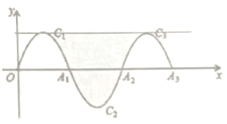
【题目】如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3,过抛物线C1,C3顶点的直线与C1、C2、C3围成的如图中的阴影部分,那么该面积为_____________
【答案】![]()
【解析】
记C1的顶点G,C2的顶点H,过G作y轴的平行线交过点H作x轴的平行线与点E,作HF⊥过两顶点的平行线于点F.然后根据,阴影部分的面积=矩形GEHF的面积求解即可.
记C1的顶点G,C2的顶点H,过G作y轴的平行线交过点H作x轴的平行线与点E,作HF⊥过两顶点的平行线于点F.
由旋转的性质知,阴影部分的面积=矩形GEHF的面积.
当-x(x-3)=0时,
x1=0,x2=3,
∴GF=0,A1=3.
∵y=-x(x-3)=![]() ,
,
∴G![]() ,
,
∴GE=![]() ,
,
∴S阴影=S矩形GEHF=![]() .
.
故答案为:![]() .
.


练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目