题目内容
已知过点(2,3)的直线y=ax+b(a≠0)不经过第四象限.设S=a+2b,则( )
A、S有最大值
| ||
B、S有最小值
| ||
| C、S有最大值6 | ||
| D、S有最小值6 |
考点:一次函数图象上点的坐标特征
专题:
分析:根据题意得出a>0,b≥0,即可推出当b=0时,S=a+2b有最小值,S的最小值为a,当b=0时,直线y=ax,把点(2,3)代入即可求得a的值,从而求得S的最小值.
解答:解:∵过点(2,3)的直线y=ax+b(a≠0)不经过第四象限,
∴a>0,b≥0,
∴当b=0时,S=a+2b有最小值为S=a,
此时y=ax,
把(2,3)代入得3=2a,解得a=
,
∴S有最小值
,
故选B.
∴a>0,b≥0,
∴当b=0时,S=a+2b有最小值为S=a,
此时y=ax,
把(2,3)代入得3=2a,解得a=
| 3 |
| 2 |
∴S有最小值
| 3 |
| 2 |
故选B.
点评:本题考查了一次函数图象上点的坐标特征,得出当b=0时,S=a+2b有最小值是关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
直角三角形的边各扩大(或缩小)相同的倍数,此三角形( )
| A、仍为直角三角形 |
| B、可能是锐角三角形 |
| C、可能是钝角三角形 |
| D、不可能是直角三角形 |
若ab>0,bc<0,则y=-
x+
经过( )
| a |
| b |
| a |
| c |
| A、第一、二、三象限 |
| B、第二、三、四象限 |
| C、第一、二、四象限 |
| D、第一、三、四象限 |
四个整数a,b,c,d互不相等,且abcd=25,求a+b+c+d的值( )
| A、1 | B、-5 | C、100 | D、0 |
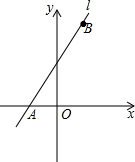 如图,已知直线l1经过点A(-1,0)和点B(1,4)
如图,已知直线l1经过点A(-1,0)和点B(1,4)