Question

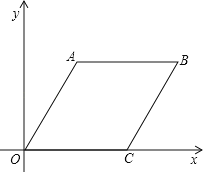
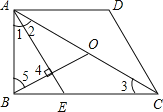
【题目】如图，在四边形ABCD中，∠ABC＝90°，AD∥BC，AE∥CD交BC于点E，AE平分∠BAC，AO＝CO，AD＝DC＝2，下面结论：①AC＝2AB；②AB＝；③S△ADC＝2S△ABE；④BO⊥AE.其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个

Answer 1

【答案】D

【解析】试题分析：∵AD∥BC，AE∥CD，

∴四边形AECD是平行四边形．

∵AD＝DC，

∴四边形AECD是菱形，

∴AE＝EC＝CD＝AD＝2，

∴∠2＝∠3．

∵∠1＝∠2，

∴∠1＝∠2＝∠3．

∵∠ABC＝90°，

∴∠1＋∠2＋∠3＝90°，

∴∠1＝∠2＝∠3＝30°，

∴BE＝AE＝1，AC＝2AB．①正确；

在Rt△ABE中，由勾股定理，得

AB＝＝＝，②正确；

∵O是AC的中点，∠ABC＝90°，

∴BO＝AO＝CO＝AC．

∵∠1＝∠2＝∠3＝30°，

∴∠BAO＝60°，

∴△ABO为等边三角形．

∵∠1＝∠2，

∴AE⊥BO．④正确；

∵S△ADC＝S△AEC＝AB·CE ，S△ABE＝AB·BE，

∵CE＝2，BE＝1，

∴CE＝2BE，

∴S△ACE＝AB·2BE

＝2×AB·BE ，

∴S△ACE＝2S△ABE，

∴S△ADC＝2S△ABE．③正确．

∴正确的个数有4个．

故选D．