题目内容
如果一个正多边形的内角是140°，则它是 边形．
考点：多边形内角与外角
专题：
分析：多边形的内角和可以表示成（n-2）•180°，因为所给多边形的每个内角均相等，故又可表示成120°n，列方程可求解．此题还可以由已知条件，求出这个多边形的外角，再利用多边形的外角和定理求解．
解答：解：设正边形的边数是n，由内角和公式，得
（n-2）×180°=n×140°．
解得n=9，
故答案为：9．
（n-2）×180°=n×140°．
解得n=9，
故答案为：9．
点评：本题考查根据多边形的内角和计算公式求多边形的边数，解答时要会根据公式进行正确运算、变形和数据处理．
练习册系列答案
备战中考寒假系列答案
相关题目
如图，已知⊙O的半径为10，弦AB长为16，则点O到AB的距离是（ ）| A、8 | B、7 | C、6 | D、5 |
正方形具有而菱形不具有的性质是（ ）
| A、对角线平分一组对角 |
| B、对角线互相垂直 |
| C、有四条对称轴 |
| D、四条边都相等 |
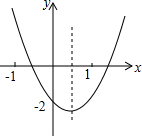二次函数y=ax2+bx+c的图象如图所示，则下列结论①abc＜0，②b2-4ac＞0，③2a+b＞0，④a+b+c＜0，⑤ax2+bx+c+2=0的解为x=-0，其中正确的有（ ）个．| A、2 | B、3 | C、4 | D、5 |
若（x+3）•（x-p）=x2+mx+36，则p、m的值分别是（ ）
| A、p=12，m=14 |
| B、p=-12，m=15 |
| C、p=-12，m=-9 |
| D、p=12，m=9 |