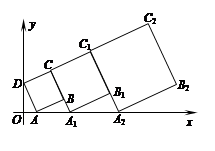Question

如图，在平面直角坐标系中，A（0，1），B（2，0），C（4，3）．

（1）求ΔABC的面积；
（2）设点P在坐标轴上，且ΔABP与ΔABC的面积相等，求点P的坐标．

Answer 1

（1）4；（2）(-6，0)或P(10，0或(0，-3)或P(0，5).

试题分析：（1）过点C作CH⊥x轴于点H，由根据梯形、三角形的面积公式求解即可；
（2）分当点P在x轴上时，设P（x，0），当点P 在y轴上时，设P（0，y），根据数轴上两点间的距离公式及三角形的面积公式求解即可.
解：（1）过点C作CH⊥x轴于点H

==4；
（2）当点P在x轴上时，设P（x，0）
由题意得
解得x=-6或10，故P(-6，0)或P(10，0)
当点P 在y轴上时，设P（0，y）
由题意得
解得y=-3或5，故P(0，-3)或P(0，5)
综上，P的坐标为(-6，0)或P(10，0或(0，-3)或P(0，5).
点评：此类问题难度较大，在中考中比较常见，一般在压轴题中出现，需特别注意.