题目内容
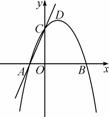
综合与探究:如图,在平面直角坐标系中,抛物线y=-x2+2x+3与x轴交于A、B两点,与y轴交于点C,点 D是该抛物线的顶点.
D是该抛物线的顶点.
(1)求直线AC的解析式及B、D两点的坐标;
(2)点P是x轴上一个动点,过P作直线l∥AC交抛物线于点Q.试探究:随着P点的运动,在抛物线上是否存在点Q,使以点A、P、Q、C为顶点的四边形是平行四边形,若存在,请直接写出符合条件的点Q的坐标;若不存在,请说明理由;
(3 )请在直线AC上找一点M,使△BDM的周长最小,求出M点的坐标.
)请在直线AC上找一点M,使△BDM的周长最小,求出M点的坐标.
解:(1)当y=0时,-x2+2x+3=0,解得x1=-1,x2=3.
∵点A在点B的左侧,∴A、B的坐标分别是(-1,0)、(3,0).(2分)
当x=0时,y=3,∴C点的坐标为(0,3).
设直线AC的解析式为y=k1x+b1(k1≠0),则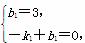
解得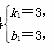 ∴直线AC的解析式为y=3x+3,(4分)
∴直线AC的解析式为y=3x+3,(4分)
∵y=-x2+2x+3=-(x-1)2+4,
∴顶点D的坐标为(1,4).(6分)
(2)抛物线上有三个这样的点Q,分别为Q1(2,3),Q2(1+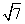 ,-3),Q3(1-
,-3),Q3(1-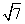 ,-3).(9分)
,-3).(9分)
(3)过点B作BB′⊥AC于点F,使B′F=BF,则B为点B关于直 线AC的对称点,连接BD交直线于AC于点M,则点M为所求.
线AC的对称点,连接BD交直线于AC于点M,则点M为所求.
过点B′作B′E⊥x轴于点E.(10分)
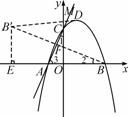
∵∠1和∠2都是∠3的余角,
∴∠1=∠2.
Rt△AOC∽Rt△AFB,
∴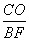 =
=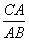 ,
,
由A(-1,0),B(3,0),C(0,3)得
OA=1,OB=3,
∴AC=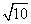 ,AB=4,
,AB=4,
∴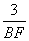 =
=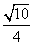 ,∴BF=
,∴BF=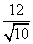 ,
,
∴BB′=2BF=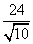 .由∠1=∠2可得Rt△
.由∠1=∠2可得Rt△ AOC∽R
AOC∽R t△B′EB,
t△B′EB,
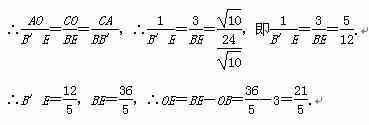 ∴B′点的坐标为
∴B′点的坐标为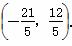
设直线B′D的解析式为y=k2x+b2(k2≠0)
∴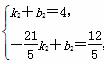 解得
解得 ∴y=
∴y=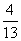 x+
x+ .
.
由 解得
解得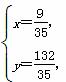 ∴M点的坐标为
∴M点的坐标为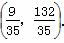

练习册系列答案
相关题目

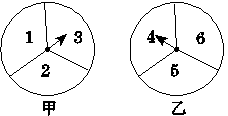
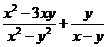 有意义的(x,y)出现的概率;
有意义的(x,y)出现的概率; D.4
D.4
 在我国古算书《周髀算经》中就有“若勾三,股四,则弦五
在我国古算书《周髀算经》中就有“若勾三,股四,则弦五