Question

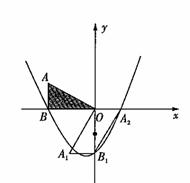
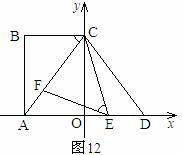
 如图12，在平面直角坐标系中，点A，C分别在轴，轴上，四边形ABCO为矩形，AB=16，点D与点A关于轴对称，tan∠ACB=，点E，F分别是线段AD，AC上的动点（点E不与点A，D重合），且∠CEF=∠ACB。

（1）求AC的长和点D的坐标；

（2）说明△AEF与△DCE相似；

（3）当△EFC为等腰三角形时，求点E的坐标。

Answer 1

解：（1）∵四边形ABCO为矩形，∴∠B=90°，

在Rt△ABC中，BC=AB÷tan∠ACB=16÷=12，

则AO=BC=12，  ∴ A（-12，0），

点D与点A关于轴对称，∴D（12，0）；

（2）∠AFE是△CEF的外角，∴∠AFE=∠FCE+∠CEF，

∵∠CEF=∠ACB，∴∠AFE=∠FCE+∠ACB=∠BCE，

∵BC∥AD， ∴∠BCE=∠DEC，∴∠AFE=∠DEC①，

∵点A与点D关于轴对称，而C，O在对称轴上，

∴△ACO与△DCO关于轴对称，

∴∠FAE=∠EDC②， 由①，②得△AEF∽△DCE；

（3）当FE=EC时，△EFC为等腰三角形，由（2），△AEF∽△DCE，∴FE:EC=AE:DC，

此时，AE=DC=AC==20，则E（8，0）；

当CF=CE时，∠CFE=∠CEF=∠ACB，则有EF∥BC，

此时，点F与A重合，则点E在D处，与已知矛盾；

当CF=FE时，∠FCE=∠CEF，又∵△AEF∽△DCE，∴∠AEF=∠DCE

∴∠FCE+∠DCE =∠CEF+∠AEF，即∠ACD=∠AEC， 而∠CAE=∠DAC，

∴△AEC∽△ACD，AE:AC=AC:AD，而AD=18，∴AE=

则E（，0），

∴当△EFC为等腰三角形时，求点E的坐标为（8，0）或（，0）。